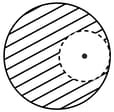
Two large spherical objects of mass $M$ each (uniformly distributed) are fixed as shown in the figure. A small point mass $m$ is projected from point $\mathrm{A}$ heading towards centre ${\mathrm{C}}_2$ of the second sphere. The minimum velocity of point mass so that it can reach up to the second object at point $\mathrm{B}$ is $\frac{n}{3}\sqrt{\frac{GM}{5R}}$. Then calculate $n$. [Neglect other gravitational forces]

A spherically symmetric gravitational system of particles has mass density $\rho =\left\{\begin{array}{l}{\rho }_0\text{ for }r\le R\\ 0\text{ for }r>R\end{array}\right.$ where, ${\rho }_0$ is a constant. A test mass can undergo circular motion under the influence of the gravitational field of particles. Its speed $v$ as a function of distance $r(0<r<\infty )$ from the centre of the system is represented by

If one wants to remove all the mass of the earth to infinity in order to break it up completely. The amount of energy that needs to be supplied will be $\frac{x}{5}\frac{G{M}^2}{R}$, where $x$ is ________.

(Round off to the Nearest Integer)

($M$ is the mass of earth, $R$ is the radius of earth, $G$ is the gravitational constant)

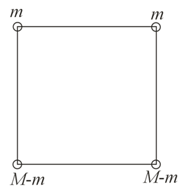
A body of mass $\left(2M\right)$ splits into four masses $\{m,m,M-m,M-m\},$ which are rearranged to form a square as shown in the figure. The ratio of $\frac{M}{m}$ for which, the gravitational potential energy of the system becomes maximum is $x : 1.$ The value of $x$ is ________.

From a solid sphere of mass $M$ and radius $R\text{,}$ a spherical portion of radius $\left(\frac{R}{2}\right)$ is removed as shown in the figure. Taking gravitational potential $V=0$ at $r=\infty ,$ the potential at the centre of the cavity thus formed is ($G=$gravitational constant)