Two particles, $1$ and $2$, move with constant velocities $v_1$ and $v_2$ along two mutually perpendicular straight lines toward the intersection point $O$. At the moment $t=0$ the particles were located at the distances $l_1$ and $l_2$ from the point $O$. How soon will the distance between the particles become the smallest? What is it equal to?

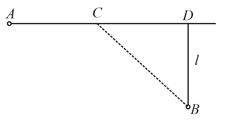
From point $A$ located on a highway (as shown) one has to get by car as soon as possible to point $B$ located in the field at a distance from the highway. It is known that the car moves in the field $\eta$ times slower than on the highway. At what distance from point $D$ one must turn off the highway?

A point travels along the $x$-axis with a velocity whose projection $v_{\mathrm{x}}$ is presented as a function of time by the plot.

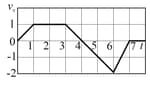
Assuming the coordinate of the point $x=0$ at the moment $t=0$, draw the approximate time dependence plots for the acceleration $w_{\mathrm{x}}$, the $x$ coordinate and the distance covered $s$.

At the moment $\mathrm{t}=0$ a particle leaves the origin and moves in the positive direction of the $x$-axis. Its velocity varies with time as $v=v_0\left(1-\frac{t}{\tau }\right)$, where $v_0$ is the initial velocity vector whose modulus equals $v_0=10.0 \mathrm{cm} {\mathrm{s}}^{-1}, \mathrm{\tau }=5.0 \mathrm{s}$. Find, 
$\left(a\right)$ the $x$ coordinate of the particle at the moments of time $6.0, 10$ and $20 \mathrm{s}$,
$\left(b\right)$ the moments of time when the particle is at the distance $10.0 \mathrm{cm}$ from the origin,

$\left(c\right)$ the distance $s$ covered by the particle during the first $4.0 \mathrm{s}$ and $8.0 \mathrm{s}$; draw the approximate plot $s\left(t\right)$.