EASY
NEET
IMPORTANT
Earn 100
Two particles separated at a horizontal distance are as shown in the figure. They are projected at the same line as shown in the figure with different initial speeds. The time after which the horizontal distance between them becomes zero is
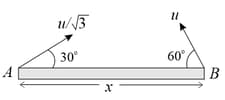

(a)
(b)
(c)
(d)none of the above.
50% studentsanswered this correctly

Important Questions on Motion in a Plane
EASY
NEET
IMPORTANT
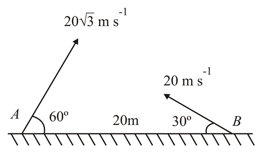
In the figure shown, the two projectiles are fired simultaneously. Find the minimum distance between them during their flight.
MEDIUM
NEET
IMPORTANT
A river is flowing from west to east at a speed of . A man on the south bank of the river, capable of swimming at in still water, wants to swim across the river in the shortest time. He should swim in a direction:
HARD
NEET
IMPORTANT
A boat moving towards east with velocity with respect to still water, and the river is flowing towards north with velocity , and the wind is blowing towards north with velocity . The direction of the flag blown over by the wind hoisted on the boat is
MEDIUM
NEET
IMPORTANT
Raindrops are falling vertically with a velocity . To a cyclist moving on a straight road, the raindrops appear to be coming with a velocity of . The velocity of the cyclist is
HARD
NEET
IMPORTANT
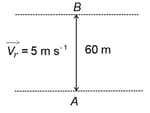
A man is crossing a river flowing with velocity of . He reaches a point directly across at a distance of in . His velocity in still water should be
HARD
NEET
IMPORTANT
A boat which has a speed of in still water crosses a river of width along the shortest possible path in . The velocity of the river water (in ) is
MEDIUM
NEET
IMPORTANT
For four particles and , the velocities of one with respect to others are given as, is towards north, is towards east and is towards south. Then is
HARD
NEET
IMPORTANT
A man crosses the river perpendicular to river flow in time seconds and travels an equal distance down the stream in seconds. The ratio of the man's speed in still water to the speed of river water will be
