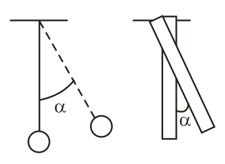
Two pendulums, a physical one in the form of a homogeneous rod and a simple one, of equal mass and length are in oscillatory motion with the same angular amplitudes. Which of the two pendulums has a higher oscillation energy?

             

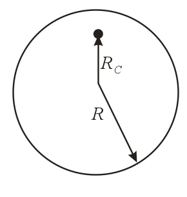
An axis passes through a disk of radius $R$ and mass $m$ at a distance $R_{\mathrm{c}}$ from the disk's center. What will be the period of oscillations of the disk about this axis (which is fixed)?

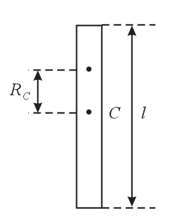
Consider a physical pendulum that is a homogeneous rod of length $l$. At what distance $R_{\mathrm{c}}$ from the center of gravity of the rod must the point of suspension lie for the oscillation period to be maximal?

A force acting on a material particle varies according to the harmonic law $F=F_0\sin \omega t$. At lime $t=0$ the velocity $v$ is zero. How do the velocity and position of the particle vary with time?

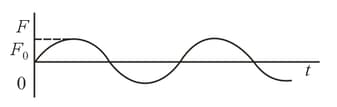
A force acting on a material particle varies according to the harmonic law $F=F_{0 }\cos \omega t$. At time $t=0$ the velocity $v$ is zero. How do the velocity and position of the particle vary with time? 

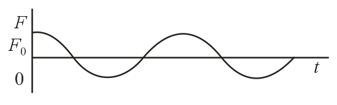
The time dependence of the amplitude of damped oscillations is presented in the figures on a semilogarithmic scale, that is, the time is laid off on the horizontal axis on a linear scale and the amplitude, on the vertical axis on a logarithmic scale. Construct the time dependence of the energy of these oscillations using the semilogarithmic scale. Set the initial values of the logarithms of the amplitude and energy of the oscillations equal.

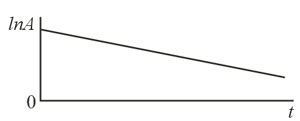
Suppose that certain damped oscillations are represented in polar coordinates. Depict these oscillations in Cartesian coordinates with the phase of the oscillations laid off on the horizontal axis and the displacement, on the vertical axis, assuming that the ratio of the sequential amplitudes of oscillations and the initial phase remain unchanged. Find the logarithmic decrement of the oscillations.

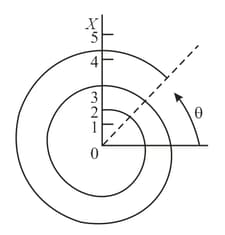
Suppose that a pendulum oscillates in a viscous medium. The viscosity of the medium and the mass and length of the pendulum are such that the oscillations are aperiodic. The pendulum is deflected from the position of equilibrium and released. How will the absolute value of the the pendulum's velocity vary with time: will it increase continuously, decrease continuously, pass through a maximum, or pass through a minimum?

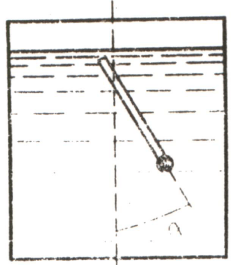
A load suspended by a spring in a viscous medium performs damped oscillations. How should one change the length of the spring (preserving all the characteristics of the spring, i.e. the thickness of the wire, the density of the turns, etc.) so that the oscillations become aperiodic? The mass of the spring is assumed to be negligible compared to the mass of the load.