Coplanar forces of magnitudes 58 N , 31 N and 26 N act at a point in the directions shown in the diagram. Given that tan α = 5 12 , find the magnitude and direction of the resultant of the three forces.

Given, tan α = 5 12 By the use of basic trigonometric sin α = 5 13 cos α = 12 13 The components of forces are shown in the following diagram The vertical component F y = 58 - 26 sin α F y = 58 - 26 × 5 13 = 48 N The Horizontal component is, F x = 26 cos α + 31 F x = 26 × 12 13 + 31 = 55 N So the magnitude of the resultant force is F = F 2 x + F 2 y F = 48 2 + 55 2 = 73 N Let the direction of the resultant force is θ tan θ = 48 55 ⇒ θ = 41 . 1 ° , from positive x direction.

HARD

AS and A Level

IMPORTANT

Earn 100

Two people drag a car of mass $1200 kg$ forward with ropes. One pulls with force $400 N$ on a bearing of $005 ° .$ One pulls with force $360 N$ on a bearing of $352 ° .$ Find magnitude of the acceleration and its direction to the nearest $0.1 ° .$

Important Questions on Forces in Two Dimensions

HARD

AS and A Level

IMPORTANT

Cambridge International AS & A Level Mathematics : Mechanics Course Book>Chapter 3 - Forces in Two Dimensions>END-OF-CHAPTER REVIEW EXERCISE 3>Q 5

A boat is in equilibrium held by a rope to the shore. The rope exerts a force $T$ at an angle $θ$ from north. The wind blows the boat with force $40 N$ in a northwest direction. The current pushes it south with a force of $50 N .$ Show that $T \sin θ = 20 \sqrt{2}$ and find an expression for $T \cos θ$ . Hence, show that $\tan θ = \frac{8 + 10 \sqrt{2}}{17}$ and find $θ$ and $T .$

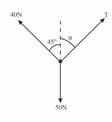
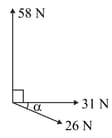
Question Image

HARD

AS and A Level

IMPORTANT

Cambridge International AS & A Level Mathematics : Mechanics Course Book>Chapter 3 - Forces in Two Dimensions>END-OF-CHAPTER REVIEW EXERCISE 3>Q 6

A car of mass

300 kg

is on a slope, which is at an angle of

5 °

to the horizontal. When it is pulled down the slope by a rope parallel to the slope with a force of

T,

it accelerates at

2 m s^{- 2} .

Find the acceleration of the car when it is pulled up the slope by a rope parallel to the slope with a force of

T .

HARD

AS and A Level

IMPORTANT

Cambridge International AS & A Level Mathematics : Mechanics Course Book>Chapter 3 - Forces in Two Dimensions>END-OF-CHAPTER REVIEW EXERCISE 3>Q 8

A girl can drag a stone block of mass

18 kg

up a slope at an angle of

13 °

to the horizontal with an acceleration of

0.7 m s^{- 2} .

Assuming this is the maximum force she can exert to drag the block, find the mass of the heaviest stone block she would be able to drag up the slope.

HARD

AS and A Level

IMPORTANT

Cambridge International AS & A Level Mathematics : Mechanics Course Book>Chapter 3 - Forces in Two Dimensions>END-OF-CHAPTER REVIEW EXERCISE 3>Q 13

A ball of mass

m kg

slides down a slope, which is at an angle of

θ °

to the horizontal. It passes two light gates

x m

apart. At the first gate, the speed of the ball is measured as

u m s^{- 1},

and at the second its speed is measured as

v m s^{- 1} .

Assuming the resistance is constant, show the resistance force has a total size of

\frac{m}{2 x} (2 xgsin θ + u^{2} - v^{2}) .

HARD

AS and A Level

IMPORTANT

Cambridge International AS & A Level Mathematics : Mechanics Course Book>Chapter 3 - Forces in Two Dimensions>END-OF-CHAPTER REVIEW EXERCISE 3>Q 14

A car of mass

m kg

is rolling down a slope of length

x m,

which is at an angle of

30 °

to the horizontal. It has a booster that provides a force of

m g N

over a distance of

1 m

, which the driver sets off at a distance

s m,

after the car starts moving. Assuming the booster is used before the end of the slope, show that the speed at the bottom of the slope is given by

v^{2} = g (x + 2)

and deduce that the final speed is independent of when the booster is applied. (Note that if the booster were applied for a fixed time rather than a fixed distance this would not be true.)

HARD

AS and A Level

IMPORTANT

Cambridge International AS & A Level Mathematics : Mechanics Course Book>Chapter 3 - Forces in Two Dimensions>END-OF-CHAPTER REVIEW EXERCISE 3>Q 15

Question Image

Coplanar forces of magnitudes $58 N, 31 N$ and $26 N$ act at a point in the directions shown in the diagram. Given that $\tan α = \frac{5}{12},$ find the magnitude and direction of the resultant of the three forces.

HARD

AS and A Level

IMPORTANT

Cambridge International AS & A Level Mathematics : Mechanics Course Book>Chapter 3 - Forces in Two Dimensions>END-OF-CHAPTER REVIEW EXERCISE 3>Q 16

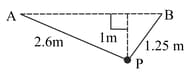
Question Image

A particle $P$ of mass $1.05 kg$ is attached to one end of each of two light inextensible strings, of lengths $2.6 m$ and $1.25 \mathrm{~m}$. The other ends of the strings are attached to fixed points $A$ and $B$, which are at the same horizontal level. $P$ hangs in equilibrium at a point $1 \mathrm{~m}$ below the level of $A$ and $B$ (see diagram). Find the tensions in the strings.

HARD

AS and A Level

IMPORTANT

Cambridge International AS & A Level Mathematics : Mechanics Course Book>Chapter 3 - Forces in Two Dimensions>END-OF-CHAPTER REVIEW EXERCISE 3>Q 17

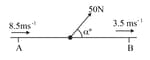
Question Image

A block of mass $60 kg$ is pulled up a hill in the line of greatest slope by a force of magnitude $50 N$ acting at an angle $α °$ above the hill. The block passes through points $A$ and $B$ with speeds $8.5 m s^{- 1}$ and $3.5 m s^{- 1}$ respectively (see diagram). The distance $A B$ is $250 m$ and $B$ is $17.5 m$ above the level of $A .$ The resistance to motion of the block is $6 N .$ Find the value of $α .$

Two people drag a car of mass 1200 kg forward with ropes. One pulls with force 400 N on a bearing of 005°. One pulls with force 360 N on a bearing of 352°. Find magnitude of the acceleration and its direction to the nearest 0.1°.

Important Questions on Forces in Two Dimensions

Learn and Prepare for any exam you want !

Two people drag a car of mass $1200 kg$ forward with ropes. One pulls with force $400 N$ on a bearing of $005 ° .$ One pulls with force $360 N$ on a bearing of $352 ° .$ Find magnitude of the acceleration and its direction to the nearest $0.1 ° .$