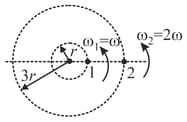
Two satellites $1$ and $2$ are orbiting with angular velocities $\omega$ and $2\omega$ relative to the centre of earth respectively, in the same plane. If the radii of their orbits are $r$ and $3r$ respectively, find the angular velocity of $1$ relative to $2\left({\overrightarrow{\omega }}_{1,2}\right)$ and angular velocity of $2$ relative to $1\left({\overrightarrow{\omega }}_{2,1}\right).$

Find the time period of the meeting of the minute hand and second hand of a clock.

Two particles $A$ and $B$ move on a circle. Initially, the particle $A$ and $B$ are diagonally opposite to each other. The particle $A$ move with angular velocity $\mathrm{\pi } \mathrm{rad} {\mathrm{s}}^{-1}$, angular acceleration $\frac{\mathrm{\pi }}{2} \mathrm{rad} {\mathrm{s}}^{-2}$ and the particle $B$ moves with constant angular velocity $2\mathrm{\pi } \mathrm{rad} {\mathrm{s}}^{-1}$. Find the time after which both the particles $A$ and $B$ will collide.

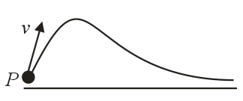
A particle $P$ moves with a constant speed $v$ in a curve as shown in the figure. Discuss the variation of magnitude of normal acceleration with time and distance.

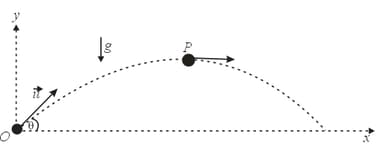
A particle is projected with velocity $u$ at an angle $\theta$ with the horizontal.
(i) Find the tangential and normal acceleration of the particle at $t=0$ and at highest point of its trajectory.
(ii) Find the radius of curvature.
(a) at $O$
(b) at highest position $P.$