HARD
Earn 100
Two side of rhombus lying in the quadrant are given by and . If the length of the longer diagonal units, find the equation of other two sides.
Important Questions on Point and Straight Line
MEDIUM
Let be a fixed point and be a moving point Let be the mid-point of and the perpendicular bisector of meets the axis at The locus of the mid-point of is
EASY
Consider a in which the relation holds. Let be the point of intersection of medians and . Then, is always
HARD
A ray travelling along the line , after being reflected from a line travels along the line . Then one of the equations of the line is
EASY
In , the bisector of intersects in . If then _____.
HARD
If the line is one of the bisectors of then value of
MEDIUM
In , is the bisector of intersects in . _____
MEDIUM
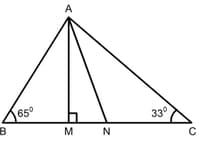
In a triangle is the altitude from on to . Draw perpendicular to and perpendicular to . Suppose and Then the length of is
EASY
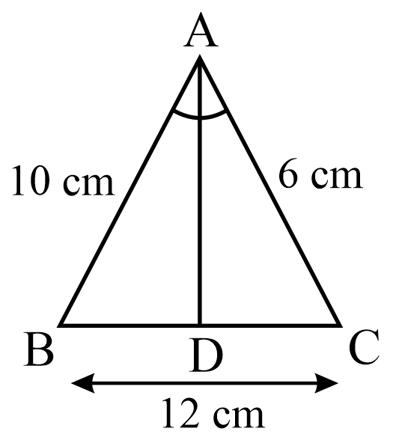
In the given figure, is the bisector of . If and . Find .
MEDIUM
If the straight line bisects the angle between a pair of lines, one of which in this pair is . Then, the equation of the other line in that pair of lines is
EASY
Let be the side-length of a triangle and be the lengths of its medians. Put Then, as vary, can assume every value in the interval
MEDIUM
and are the points on sides and , respectively of and intersect each other at T. If and , then
HARD
Two equal sides of an isosceles triangle are and and its third side passes through the point . The equation of the third side is
EASY
In , and. If bisector of meets at . Then is
HARD
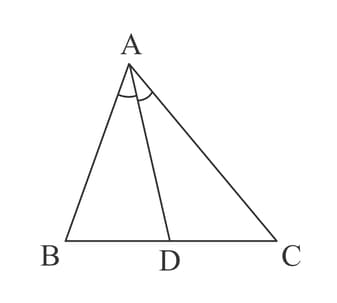
In , it is given that Find in degrees.
MEDIUM
In the given fig. and is the bisector of . If and , then the value of will be
HARD
Let be the slopes of two adjacent sides of a square of side such that . If one vertex of the square is , where and the equation of one diagonal is , then is equal to
MEDIUM
Let the point be at a unit distance from each of the two lines , and . If lies below and above , then is equal to
MEDIUM
Let be an acute-angled triangle in which . From the vertex draw the altitude the angle bisector and the median , with lying on . Then,
MEDIUM
Statement-I: Two lines which pass through a given fixed point and are equally inclined to two other lines passing through the same point, are always perpendicular to each other.
Statement-II: Angle bisectors of two intersecting lines are always perpendicular to each other.
MEDIUM
The equation of the plane which bisects the angle between the planes and which contains the origin is