MEDIUM
MHT-CET
IMPORTANT
Earn 100

Two springs each of spring constant k are attached to the sphere, one at centre and the other at the top as shown. The radius of the sphere is R, and its mass is M. If the sphere rolls on the ground without slipping, the angular frequency of oscillation of the sphere would be

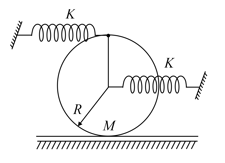
Question Image

50% studentsanswered this correctly

Important Questions on Oscillations

EASY
MHT-CET
IMPORTANT
MHT-CET TRIUMPH Physics Multiple Choice Questions Part - 1 Based on Std. XI & XII Syllabus of MHT-CET>Chapter 12 - Oscillations>Evaluation Test>Q 8
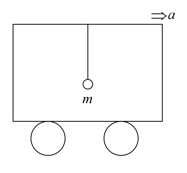
A simple pendulum is vertically hanging in a car. The mass of the bob is m. If the car is given an acceleration a suddenly, find the maximum displacement of the bob.
Question Image
EASY
MHT-CET
IMPORTANT
MHT-CET TRIUMPH Physics Multiple Choice Questions Part - 1 Based on Std. XI & XII Syllabus of MHT-CET>Chapter 12 - Oscillations>Evaluation Test>Q 9
What will be the momentum v/s position plot of a spring mass oscillator kept on a rough horizontal surface? What should be the plot for one cycle?
MEDIUM
MHT-CET
IMPORTANT
MHT-CET TRIUMPH Physics Multiple Choice Questions Part - 1 Based on Std. XI & XII Syllabus of MHT-CET>Chapter 12 - Oscillations>Evaluation Test>Q 10
A pendulum suspended from the roof of a railway carriage travelling at a speed v m s-1 around a curve of radius a metres makes n oscillations per second. If the same pendulum makes n1 oscillations per second when the carriage is stationary, what is the value of v2?
HARD
MHT-CET
IMPORTANT
MHT-CET TRIUMPH Physics Multiple Choice Questions Part - 1 Based on Std. XI & XII Syllabus of MHT-CET>Chapter 12 - Oscillations>Evaluation Test>Q 11
A circular disc has a tiny hole in it, at a distance z from its centre. Its mass is M and radius R·R>z. A horizontal shaft is passed through the hole and held fixed so that the disc can freely swing in the vertical plane. For small disturbance, the disc performs S.H.M. whose time period is minimum for z.
MEDIUM
MHT-CET
IMPORTANT
MHT-CET TRIUMPH Physics Multiple Choice Questions Part - 1 Based on Std. XI & XII Syllabus of MHT-CET>Chapter 12 - Oscillations>Evaluation Test>Q 12
If the length of a simple pendulum is comparable to the radius of the earth, then find the time period for oscillation.
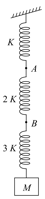
MEDIUM
MHT-CET
IMPORTANT
MHT-CET TRIUMPH Physics Multiple Choice Questions Part - 1 Based on Std. XI & XII Syllabus of MHT-CET>Chapter 12 - Oscillations>Evaluation Test>Q 13
The figure alongside shows a system of springs connected to a mass M. The amplitude of oscillation of this system would be mg3k. What will be the ratio of the amplitudes of oscillation of points A and B?
Question Image
MEDIUM
MHT-CET
IMPORTANT
MHT-CET TRIUMPH Physics Multiple Choice Questions Part - 1 Based on Std. XI & XII Syllabus of MHT-CET>Chapter 12 - Oscillations>Evaluation Test>Q 14
A block of mass M is attached to three springs, A, B & C having force constants K, K and 3K as shown in the figure. If the block is slightly pushed against spring C. Then find the frequency of oscillations,
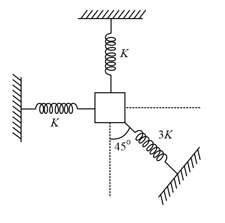
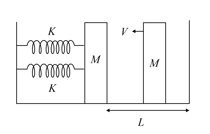
Question Image
MEDIUM
MHT-CET
IMPORTANT
MHT-CET TRIUMPH Physics Multiple Choice Questions Part - 1 Based on Std. XI & XII Syllabus of MHT-CET>Chapter 12 - Oscillations>Evaluation Test>Q 15
The right block in the figure moves at a speed v towards the left block placed in equilibrium. All the surfaces are smooth and all the collisions are elastic. Find the time period of the motion.
Question Image