HARD
JEE Main
IMPORTANT
Earn 100
Two stones are thrown up simultaneously from the edge of a cliff high with an initial speed of and respectively. Which of the following graph best represents the time variation of the relative position of the second stone with respect to the first? (Assume stones do not rebound after hitting the ground and neglect air resistance, take )(the figure are schematic and not drawn to scale)
(a)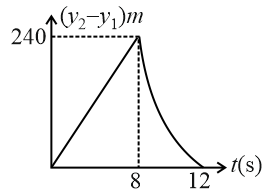

(b)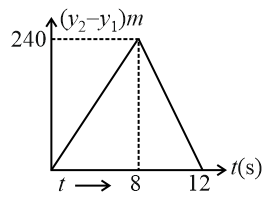

(c)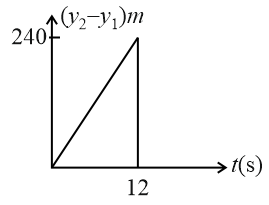

(d)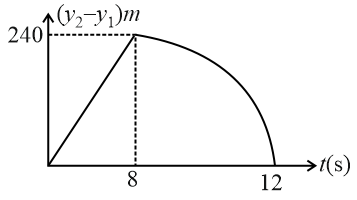

50% studentsanswered this correctly

Important Questions on Kinematics
MEDIUM
JEE Main
IMPORTANT
A bullet loses of its velocity passing through one plank. Considering uniform retardation, the number of such planks that are required to stop the bullet can be:
MEDIUM
JEE Main
IMPORTANT
The position of a projectile launched from the origin at t = 0 is given by at t = 2s. If the projectile was launched at an angle from the horizontal, then is (take g = 10 ms-2).
HARD
JEE Main
IMPORTANT
From a tower of height H, a particle is thrown vertically upwards with a speed u. The time taken by the particle, to hit the ground, is n times that taken by it to reach the highest point of its path.The relation between H, u and n is :
EASY
JEE Main
IMPORTANT
A projectile is given an initial velocity of , where is along the ground and is along the vertically upward direction. If , the equation of its trajectory is :
MEDIUM
JEE Main
IMPORTANT
Let and The value of is:
MEDIUM
JEE Main
IMPORTANT
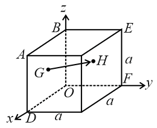
In the cube of side shown in the figure, the vector from the central point of the face to the central point of the face will be:
MEDIUM
JEE Main
IMPORTANT
Two vectors and have equal magnitudes. The magnitude of is times the magnitude of . The angle between and is:
MEDIUM
JEE Main
IMPORTANT
Two forces and , of magnitude and , respectively, are at an angle with each other. If the force is doubled, then their resultant also gets doubled. Then, the angle is:
