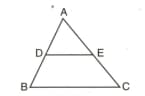
Using $SAS$ property, prove that triangle formed by joining the midpoints of sides of a triangle is similar to other four triangles.

In the given figure, $△ABC$ and $△DEF$ are similar, $BC=3 \mathrm{cm}$, $EF=4 \mathrm{cm}$ and area of $△ABC=54 \mathrm{sq}. \mathrm{cm}$. Determine the area of $△DEF$.

In two similar triangles $ABC$ and $DEF$, $AC=10 \mathrm{cm}$ and $DF=8 \mathrm{cm}$. Find the ratio of the areas of triangle $ABC$ to triangle $DEF$.

In the given figure, $△ABC~△DEF$. If $AB=2DE$ and area of $△ABC$ is $56 \mathrm{sq}. \mathrm{cm}$, find the area of $△DEF$.

In two similar triangles $ABC$ and $PQR$, if their corresponding altitudes $AD$ and $PS$ are in the ratio $4:9$, if the ratio of the area of $△ABC$ to that of $△PQR$ is $m:n,$ then find the value of $m+n.$

In the given figure, $PB$ and $QA$ are perpendiculars to segment $AB$. If $PO=5 \mathrm{cm}$, $QO=7 \mathrm{cm}$ and area of $△POB=150 {\mathrm{cm}}^2$, find the area of $△QOA$.

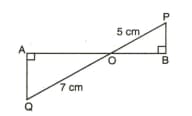
In figure, $ABC$ is a triangle and $PQ$ is a straight line meeting $AB$ in $P$ and $AC$ in $Q$. If $AP=1 \mathrm{cm}$, $BP=3 \mathrm{cm}$, $AQ=1.5 \mathrm{cm}$, $CQ=4.5 \mathrm{cm}$, prove that area of $△APQ=\frac{1}{16}$ area of $△ABC$.

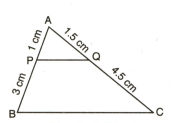
In the figure, $DE$ is parallel to $BC$ and $AD:DB=2:3$. Determine area $\left(△ADE\right):$area $\left(△ABC\right)$.

If the area of the equilateral triangle described on the side of square is $48 {\mathrm{cm}}^2$. If the area of the equilateral triangle described on its diagonal is $k {\mathrm{cm}}^2$, then find the value of $k$.