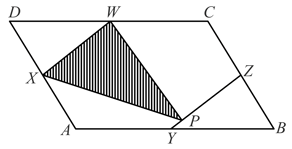
and are the midpoints of the four sides of parallelogram is a point on the line segment . What percent of the area of parallelogram is a triangle ?


Important Points to Remember in Chapter -1 - Geometry from Embibe Experts Non-Routine Mathematics Resource Book-2 for PRMO Solutions
TRIANGLES
-
Angle: A measure of geometric span between two rays with a common initial point.
It is measured in degrees/ radians/ grades etc.
2. Types of angles:-
(a) Zero angle - Angle measure of
(b) Acute angle - Angle measure between and
(c) Right angle - Angle measure of
(d) Obtuse angle - Angle measure between and
(e) Straight angle - Angle measure of
(f) Reflex angle - Angle measure between and
(g) Complete angle - Angle measure of
3. Pair of angles:
(a) Complementary angles - Two angles whose sum is
(b) Supplementary angles - Two angles whose sum is
(c) Adjacent Angles - Two angles with a common arm.
Here and are adjacent angles as they have a common arm .
(d) Linear Pair of Angles - Angles which are pair wise adjacent and combined, form a straight line.
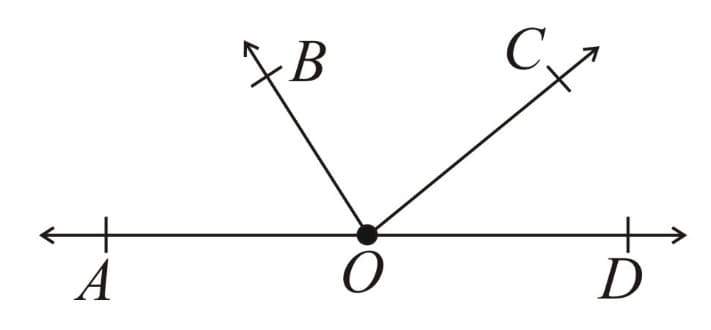
Here & and & are pair wise adjacent and all combined, form a straight line. So are linear pair of angles.
(e) Vertically opposite Angles - When two lines intersect the angles on the opposite sides of point of intersection are called vertically opposite angles.
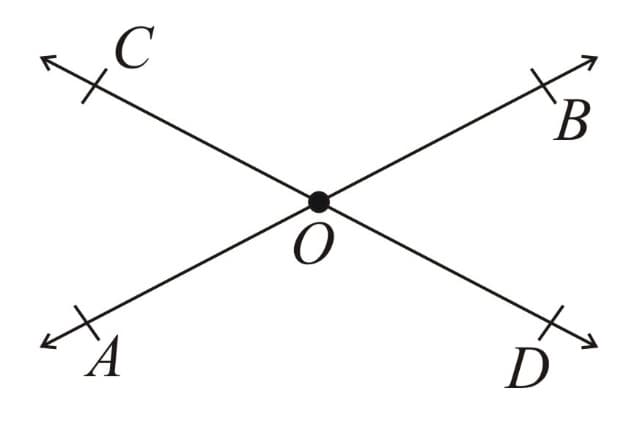
Here, & and & are vertically opposite angles.
4. Vertically opposite angles theorem: It states that the vertically opposite angles, formed on intersection of two lines, are equal.
i.e.
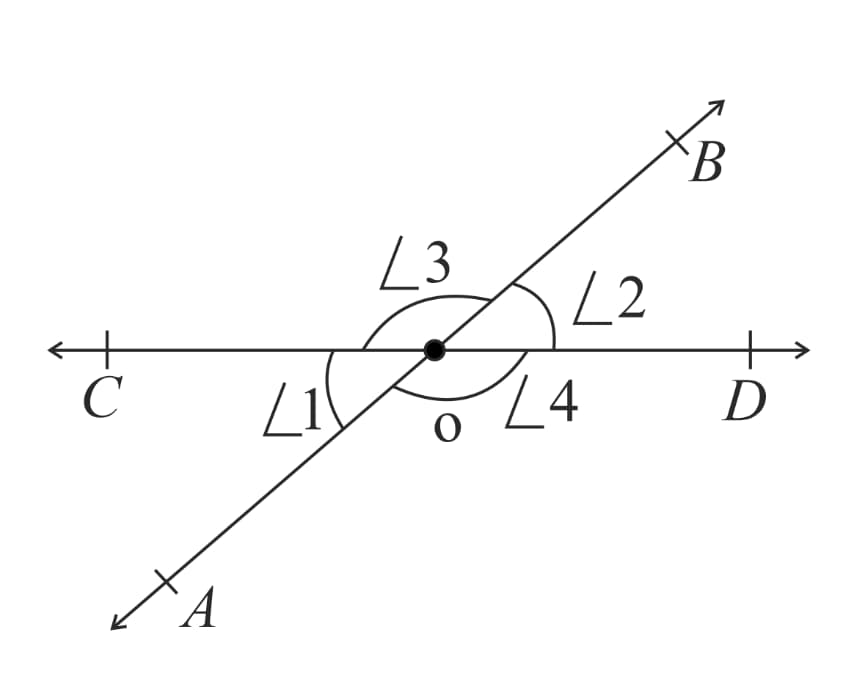
Here, (Linear pair)
(Linear pair)
From and ,
Similarly,
5. Angles made by a transversal on two lines:
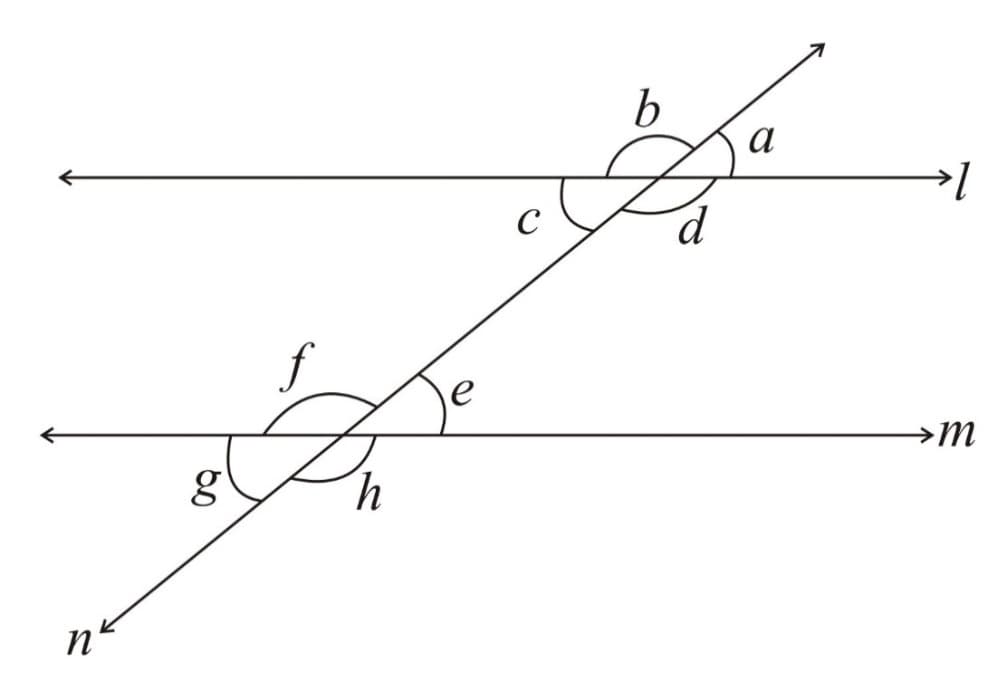
(a) Interior angles - are interior angles
(b) Exterior angles - are exterior angles
(c) Corresponding angles - are corresponding angles.
(d) Alternate Interior Angles - are alternate interior angles
(e) Alternate Exterior Angles - are alternate exterior angles.
(f) Interior Angles on the same side of transversal or co-interior angles - are co-interior angles.
6. Corresponding Angles Axiom: If a transversal intersects two parallel lines, then each pair of corresponding angles are equal and vice-versa.
7. Alternate Interior Angles theorem: If a transversal intersects two parallel lines, each pair of alternate interior angles is equal and vice versa.
i.e.
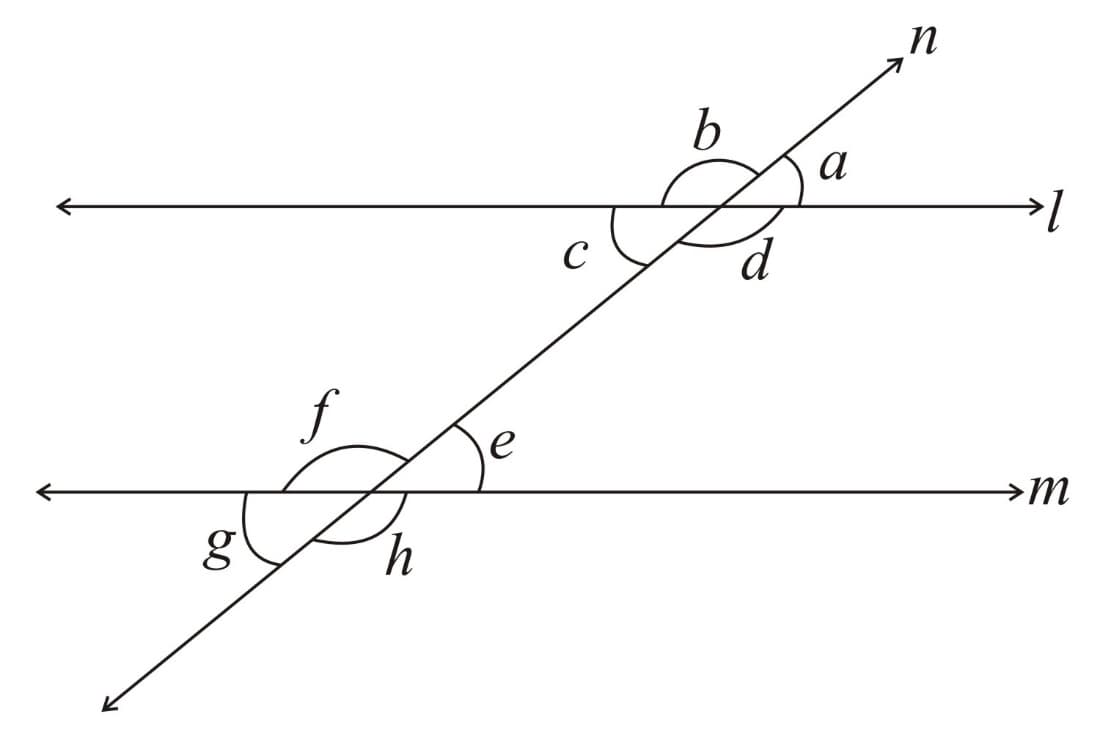
Here, and is transversal, and (corresponding angles axiom)
Now, (vertically opposite angles)
From and ,
, i.e. alternate interior angles are equal.
Similarly,
8. Co- Interior Angles theorem: If a transversal intersects two parallel lines, each pair of co-interior angles is supplementary.
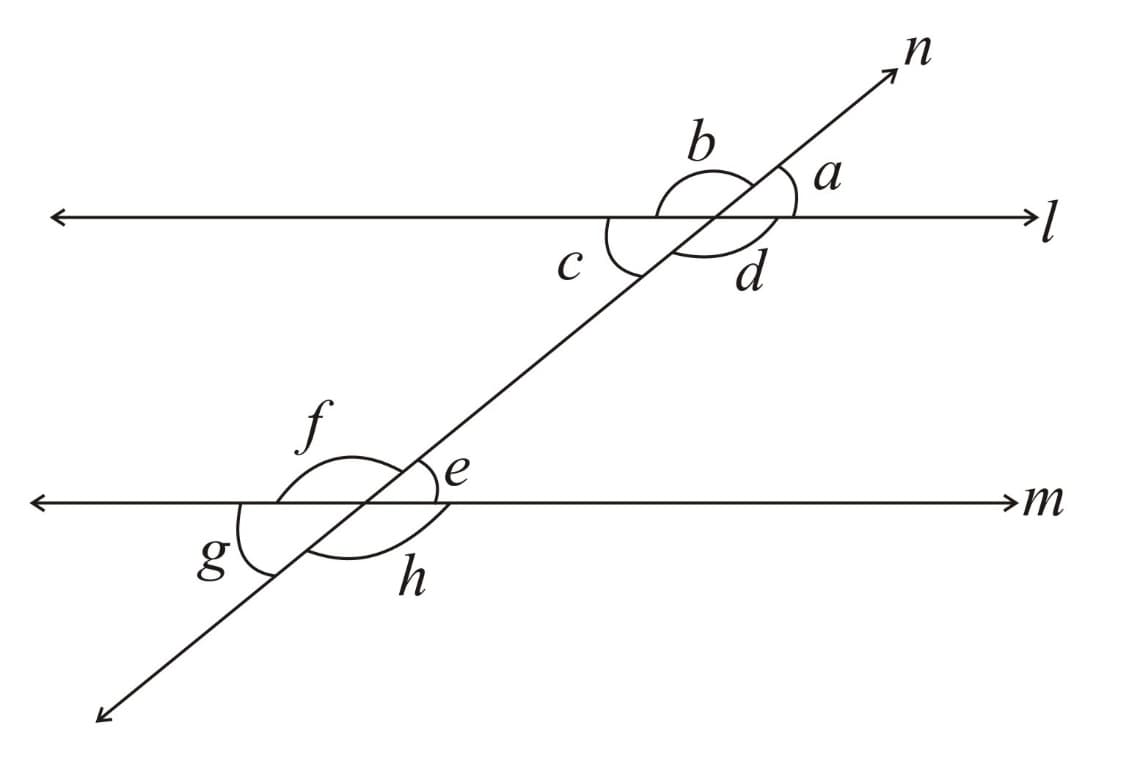
Here, and is the transversal.
Now, (corresponding angles)
(Linear pair)
From and ,
, i.e. co-interior angles are supplementary.
Similarly,
9. Triangle: A closed plane figure with three vertices and three sides.
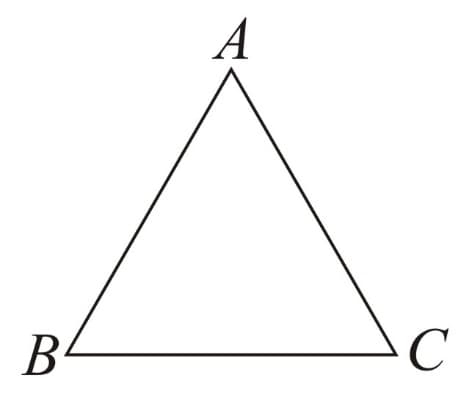
Here, are the vertices and are the sides of the triangle. The angles are .
Also,
is the side opposite to and vice- versa;
is the side opposite to ind vice-versa;
is the side opposite to and vice-versa.
10. Types of triangles:
(A) Based on sides -
(a) Scalene Triangle: When all sides are unequal in length.
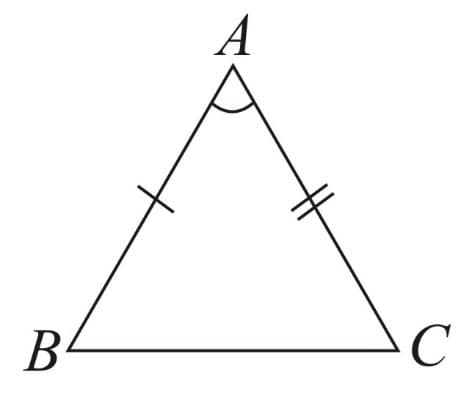
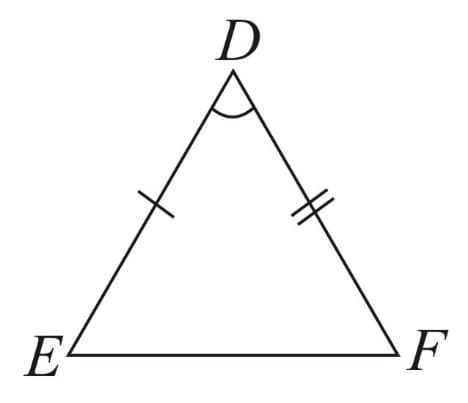
(b) Isosceles Triangle: When exactly two sides are equal in length.
For
(i)
(ii) If , then and vice-versa.
(c) Equilateral Triangle: When all sides are equal in length.
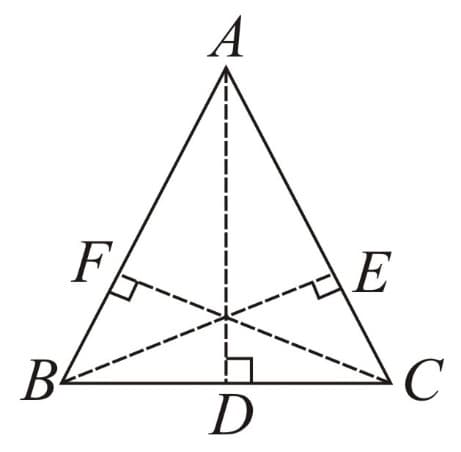
For
(i)
(ii) If , then and vice - versa. Similarly, for and
(iii) Area sq. units
(B) Based on Angles –
(a) Acute Angled - When all angles are acute angles.
(b) Obtuse Angled - When one angle is obtuse angle.
(c) Right Angled - When one angle is right angle (i.e. ).
11. Pythagoras Theorem: In a right angled triangle, sum of squares of the perpendicular sides is equal to square of hypotenuse.
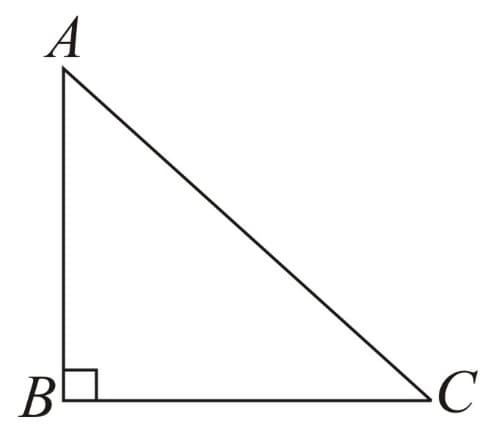
Here, right angle is at so hypotenuse is the side opposite to it, i.e.
A set of three such positive integers is called PYTHAGOREAN TRIPLET.
If further, the triangle is called Right Isosceles Triangle with
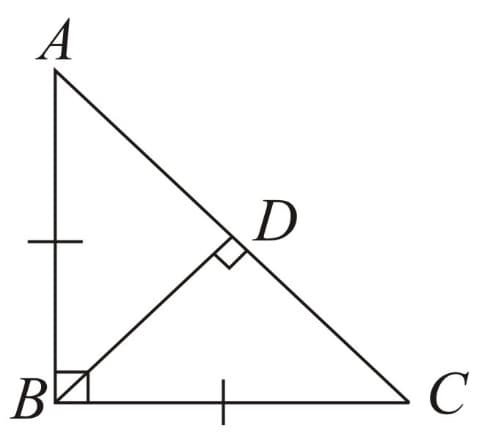
Also, if then and vice - versa.
12. Angle Sum Property:
(A) For interior angles - sum of all interior angles of a triangle is
(B) For exterior angles - Sum of all exterior angles of a triangle is
13. Exterior Angle Property: Exterior angle is equal to the sum of interior opposite angles.
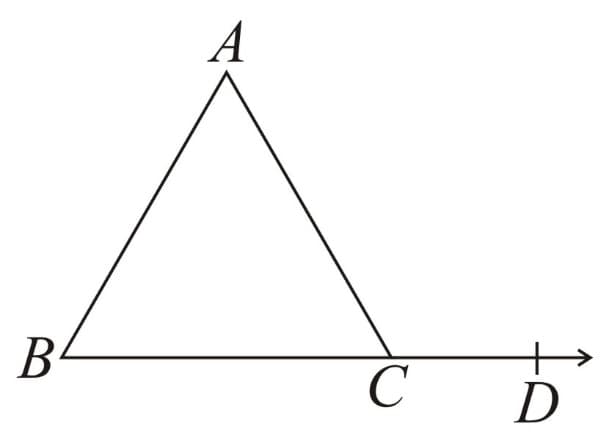
Here, exterior angle
14. Special parts of a triangle:
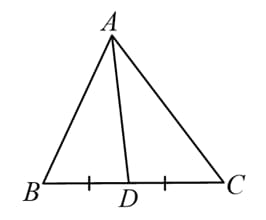
(A) Median - line segment joining a vertex to the mid-point of its opposite side.
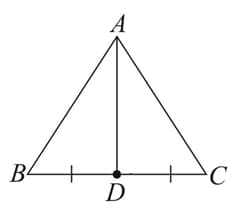
Here, is the median as
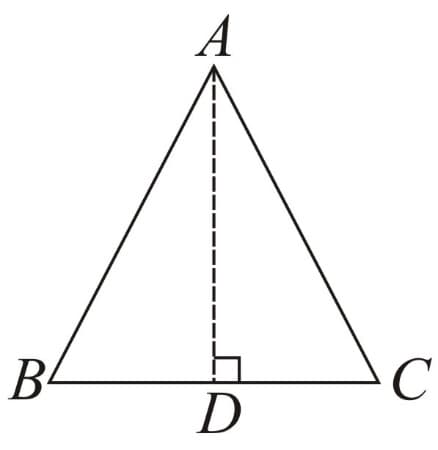
(B) Altitude - Line segment joining a vertex to the foot of perpendicular on its opposite side.
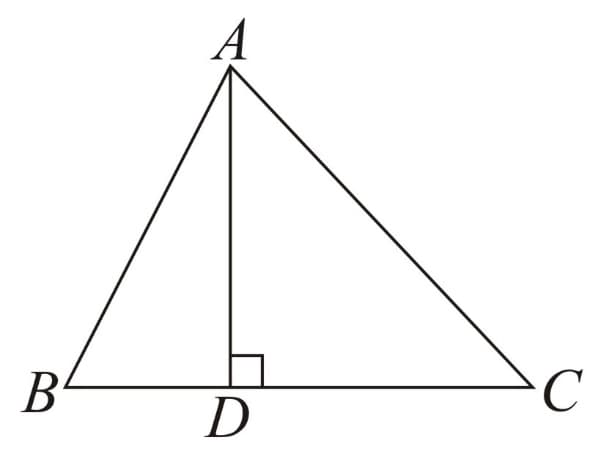
Here, is the altitude as .
15. Special Paints of a triangle:
(A) Centroid - Point of concurrence of all three medians.
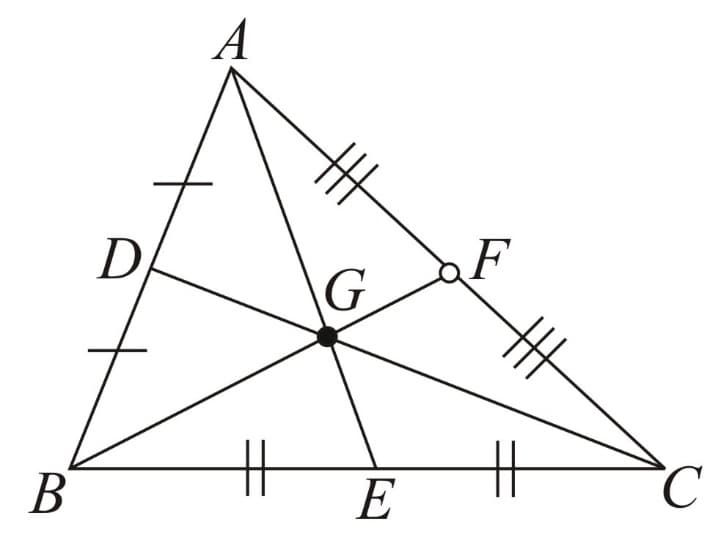
Here, are medians and is the centroid.
-
Always lies inside the triangle.
(B) Orthocentre - Point of concurrence of all three altitudes.
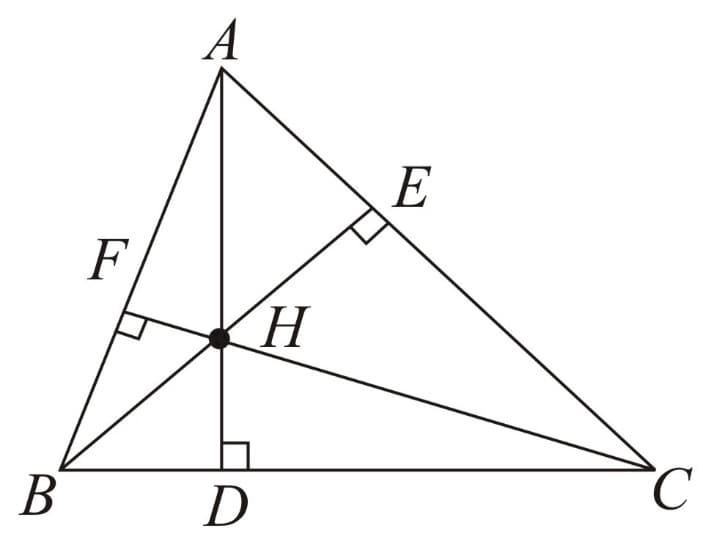
Here, are the altitudes and is the orthocentre.
-
Lies inside an acute angled triangle.
-
Lies outside an obtuse angled triangle
-
Lies at the right angle vertex in right angled triangle.
(C) Circumcentre - Point of concurrence of perpendicular bisectors of all three sides.
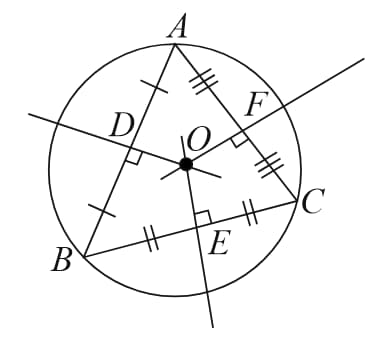
Here, are perpendicular bisectors of respectively and is the circumcentre.
-
Vertices lie on the circle called circumcircle with centre
-
called circumradius (i.e. radius of the circumcircle)
-
Lies inside an acute angled triangle
-
Lies outside an acute angled triangle
-
Lies at the mid- point of hypotenuse in a right angled triangle.
(D) Incentre - Point of concurrence of all bisectors of the three interior angles of the triangle.
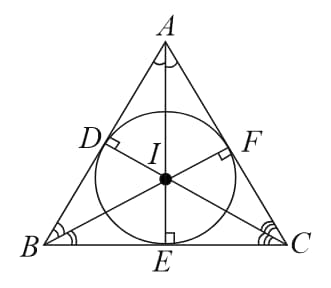
Here, are the angle bisectors of respectively and is the incentre.
-
Always lies inside a triangle.
-
A circle, called incircle, with centre touches the sides at respectively such that
-
called inradius (or radius of the incircle).
16. Internal Angle Bisector Theorem:
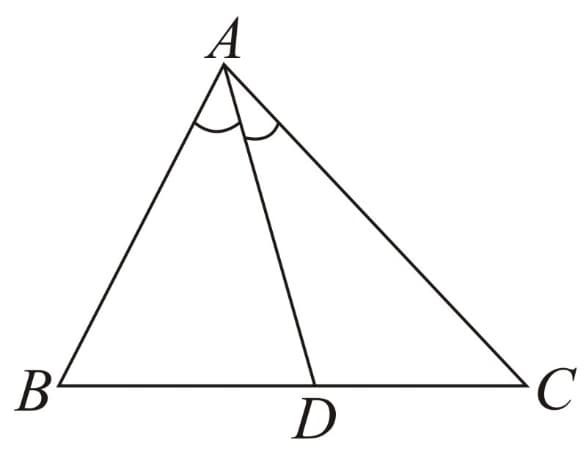
In , if bisects ; then .
17. Congruence of triangles: Two triangles are said to be congruent if they overlap each other completely, i.e. their corresponding sides and angles are equal.
-
Congruence of triangles is represented by the symbol
-
If then and (using corresponding parts of congruent triangles or c.p.c.t.)
18. Criteria for congruency:
-
Side - Angle - Side i.e. rule:
If two corresponding sides of two triangles and the angles included between the two sides are equal, then the triangles are congruent.
Here,
So, (SAS rule)
(B) Angle- Side - Angle i.e. ASA rule:
If two corresponding angles and the side included between them are equal in two triangles, then the triangles are congruent.
i.e.
If
Then (ASA rule)
(C) Angle - Angle - Side i.e. AAS rule:
If two corresponding angles and the side not included between them are equal in two triangles, then the triangles are congruent.
i.e. If
Then (AAS rule)
(D) Side - Side - Side i.e. SSS rule:
If all three corresponding sides in two triangles are equal, then the triangles are congruent.
i.e.
If
Then (SSS rule)
(E) Right - Hypotenuse - Side i.e. RHS rule:
In two right angled triangles, if the hypotenuses and either of the remaining perpendicular sides are equal, then the two right angled triangles are congruent.
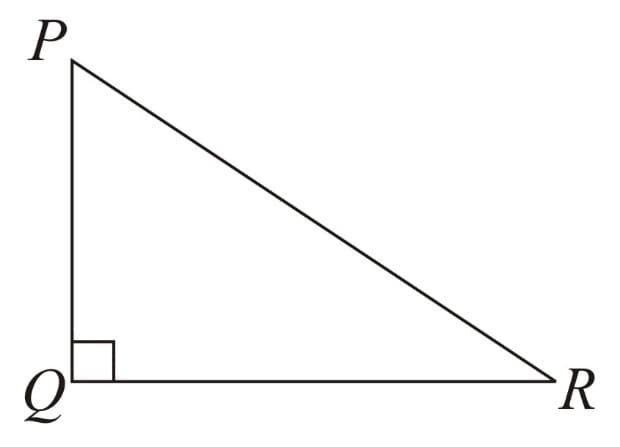
i.e.
If
(Hypotenuse)
(perpendicular)
Then (RHS Rule)
19. Similarity of Triangles: When two triangles have the same shape but different sizes, i.e. the two triangles can be overlapped by scaling one of them, in proportion, then the triangles are said to be similar. Similarity is represented by the symbol
If then and (Using corresponding parts of similar triangles or c.p.s.t.)
20. Criterias for similarity:
(A) Angle-Angle (AA) or Angle- Angle- Angle (AAA):
If two corresponding angles of two triangles are equal, then the triangles are similar.
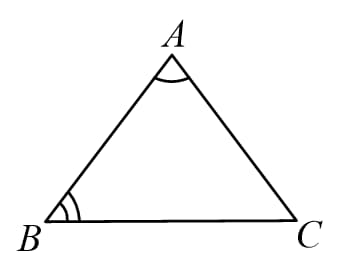
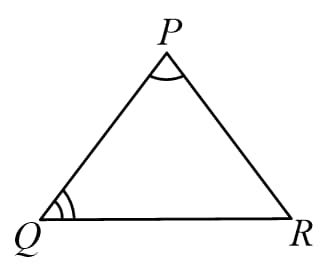
i.e.
if
Then (AA rule)
Note: If two angles in two triangles are equal, then the third angle will automatically be equal (using angle sum property of triangle). So, AA rule and AAA rule are the same.
-
Side- Side- Side (SSS) rule:
If ratio of all three corresponding sides is equal then the triangles are similar.
i.e.
If ,
Then (SSS rule)
(C) Side-Angle-Side (SAS) rule:
If ratio of two correspoinding sides in two triangles are equal and the included angles are also equal, then the triangles are similar.
i.e.
If
Then (SAS rule)
(D) Right-Hypotenuse-Side (RHS) rule:
If ratio of hypotenuse and one of the remaining sides in two right angled triangles are equal, then the right angled triangles are similar.


i.e.
If ,
Then (RHS rule).
21. Some results related to similar triangles:
If then:
(A) The ratio of corresponding medians is equal to the ratio of sides.
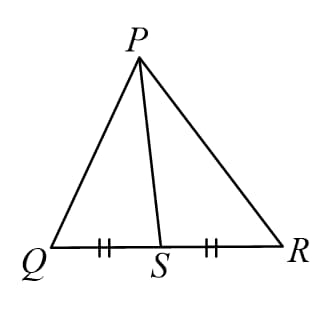
i.e.
Similarly, for remaining medians.
(B) The ratio of corresponding altitudes is equal to the ratio of sides.
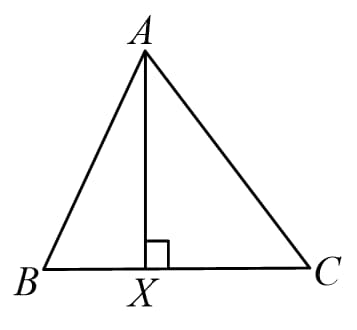
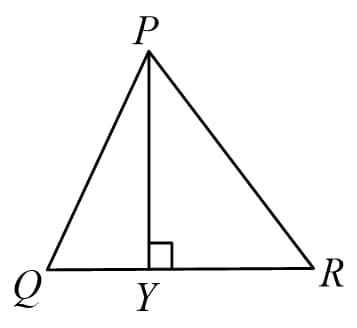
i.e.
Similarly, for remaining altitudes also.
(C) The ratio of corresponding interiors angle bisectors is equal to the ratio of sides.
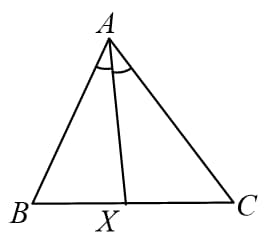
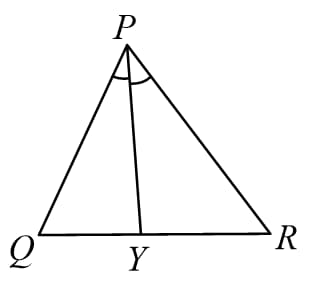
i.e.
Similarly, for remaining interior angle bisectors also.
(D) The ratio of area is equal to square of the ratio of sides.
i.e.
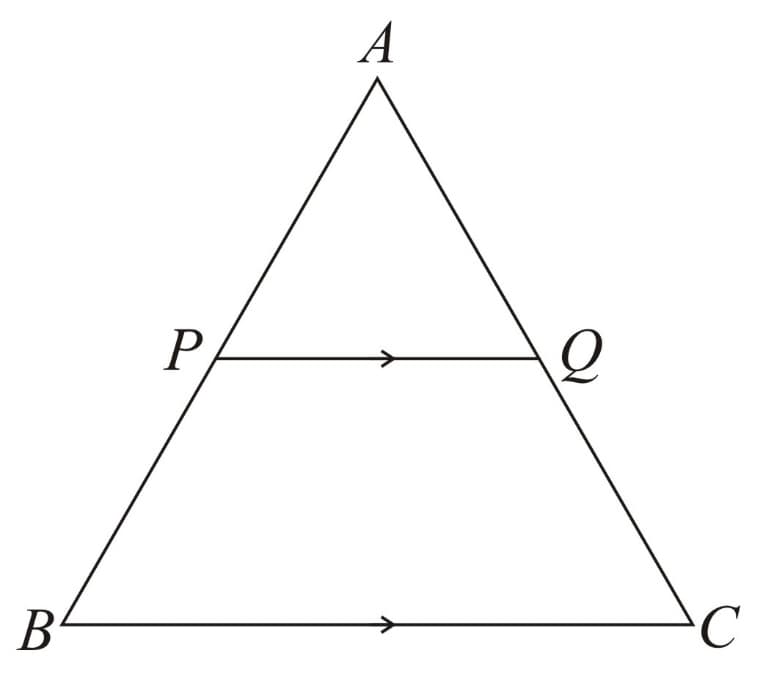
22. Basic Proportionality Theorem (BPT) or Thales theorem:
If a line is drawn parallel to a side of a triangle, intersects the remaining two sides in distinct points, then these two sides are divided in the same ratio.
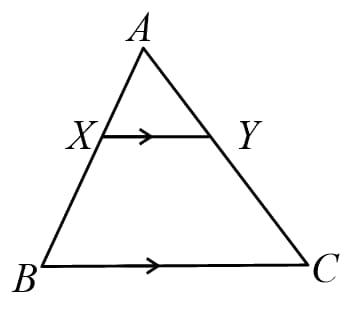
i.e. if then
23. Mid-point theorem: The line segment joining the mid-point of any two sides of a triangle is parallel to the third side and also half of it.
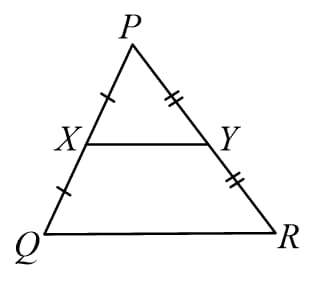
i.e. if and
Then and
24. Converse of Mid-Point Theorem: If a line is drawn parallel to a side of a triangle, through the mid-point of another side, then it bisects the third side of the triangle.
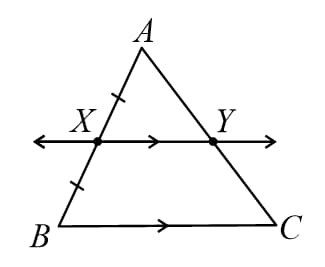
i.e. if and
Then
25. Inequalities in Triangles:
In the ,
(i) Sum of any two sides of a triangle is greater than the third side.
i.e.
(ii) Magnitude of difference of any two sides is smaller than the third side.
i.e.
(iii) Side opposite to the larger angle is longer and vice-versa.
i.e. and so on.
(iv) Side opposite to the smaller angle is shorter and vice-versa.
i.e. and so on.
Ceva’s Theorem:
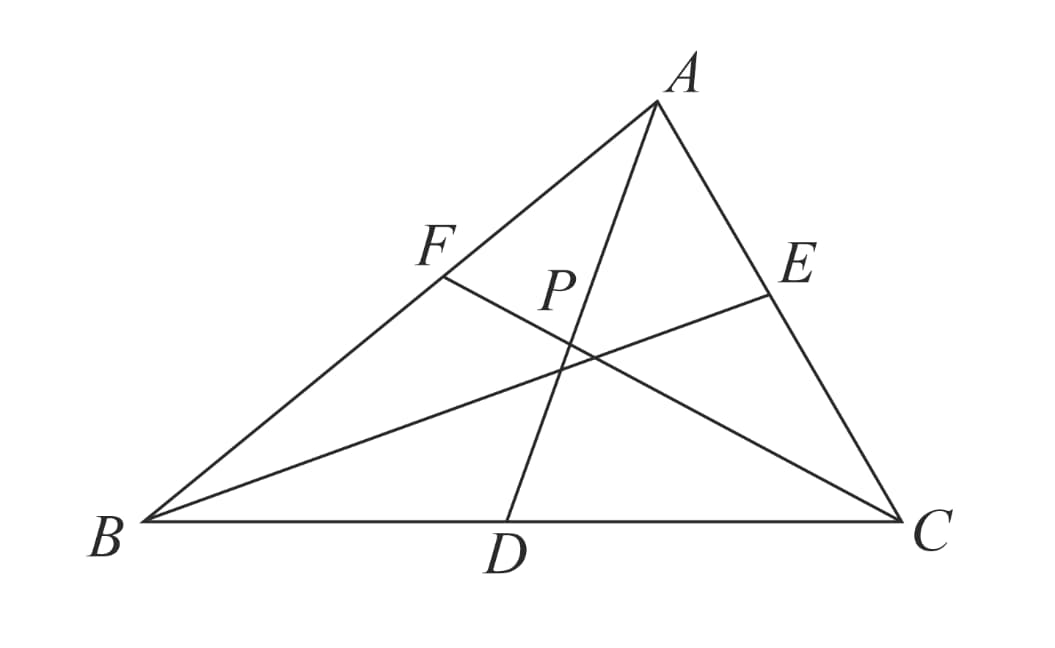
Given a triangle with a point inside the triangle, continue lines to hit at respectively.
Ceva's theorem states that
Morley's Trisector Theorem:
Theorem states that the points of intersection of the adjacent trisectors of the angle of any triangle are the vertices of an equilateral triangle.
Triangle Proportionality Theorem:
If a line is drawn parallel to any one side of a triangle in such a way that it intersects the other two sides in two distinct points then the other two sides of the triangle are divided in the same ratio.
Van Aubel's Theorem:
The area of a triangle with a fixed baseand varying apex changes in proportion to its altitude.
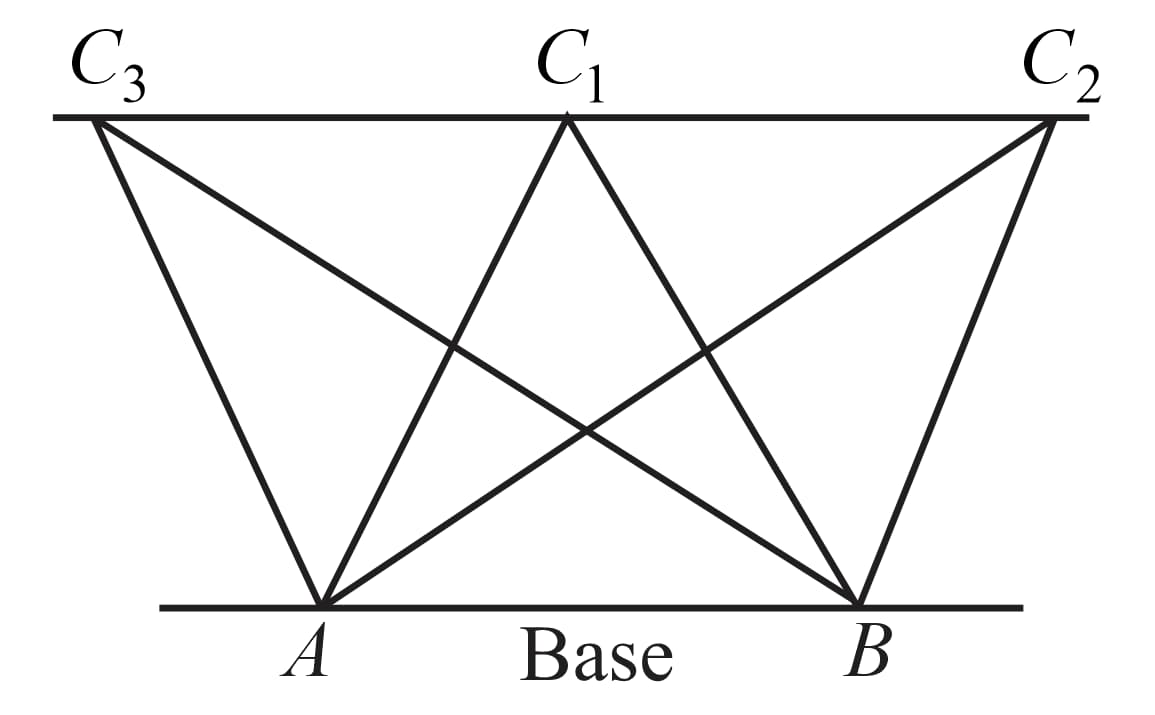
Area of is same for as altitude (height of triangle is same).
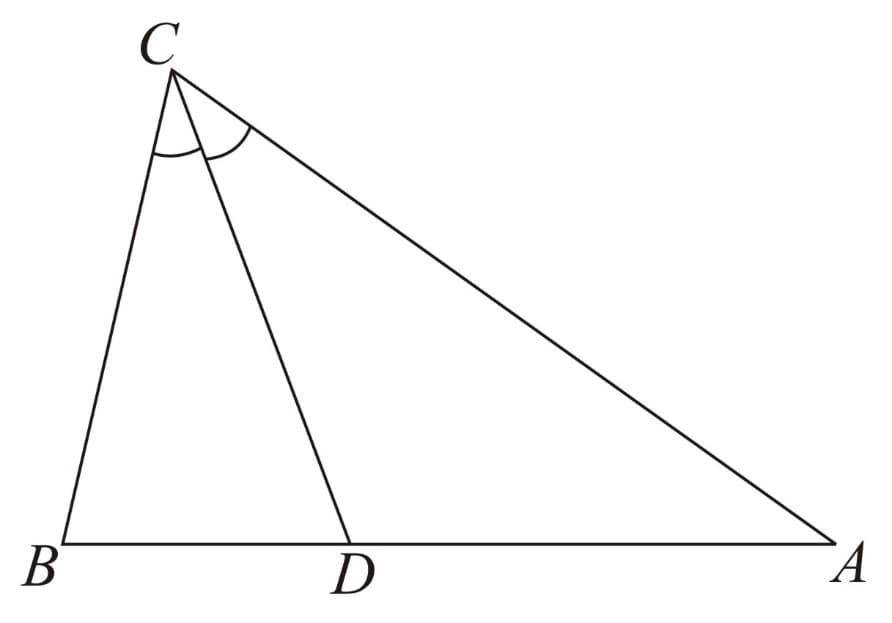
Angle Bisector Theorem:
If an interior angle of a triangle is bisected, the bisector divides the opposite side into segments whose lengths have the same ratio as the lengths of the noncommon adjacent sides of the respective bisected angle. That is,
The converse of the theorem above is also true. More precisely, consider a triangle where we are given a point on side
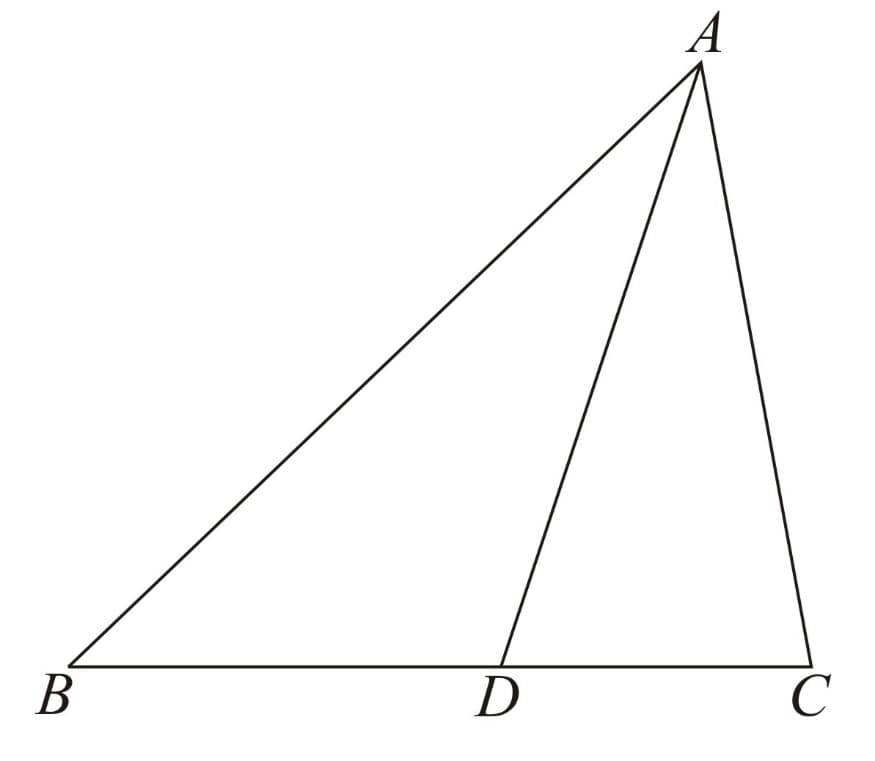
If we are given that the lengths of the line segments satisfy
we know that point lies on the bisector of the interior angle at vertex in triangle
Consider which is an exterior angle of triangle at vertex is bisected by that intersects the extension of the side of the triangle opposite which is at a point as shown in the following diagram.
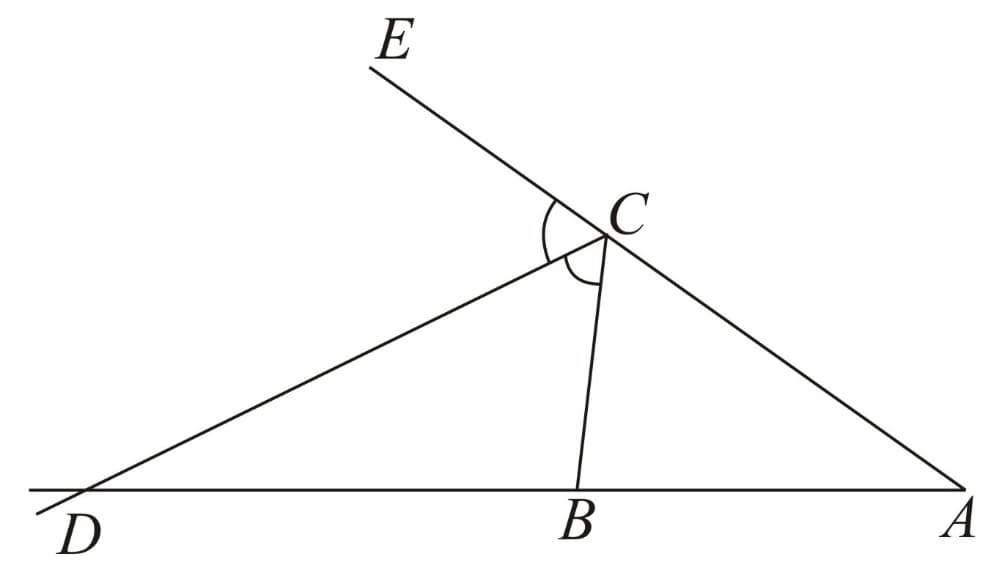
We have the following identity:
In any triangle if is the angle bisector of angle then we have
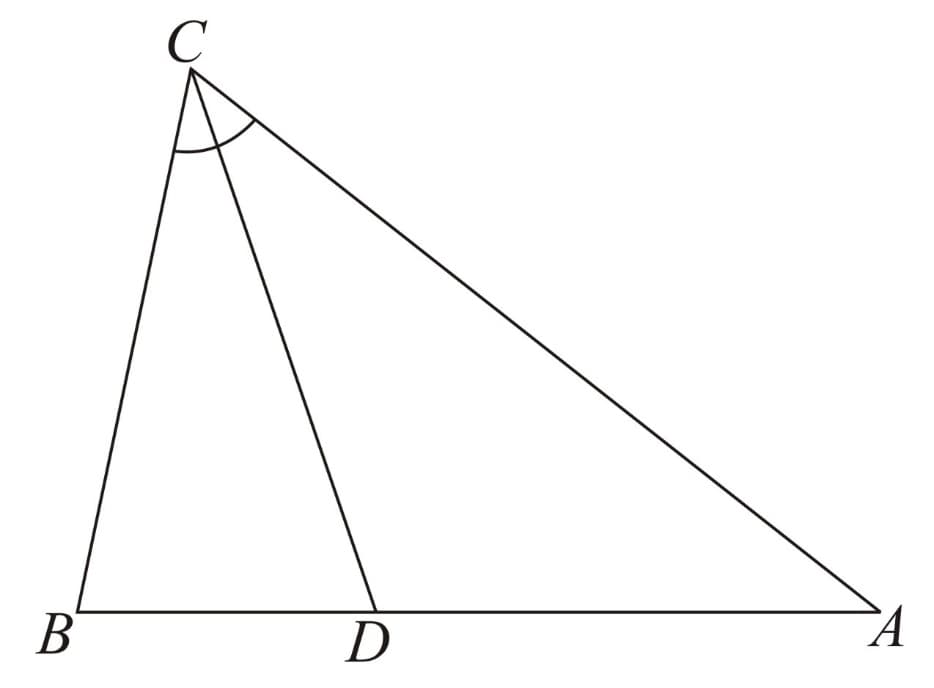
Triangle Inequality Theorem for an Acute Triangle:
Just like the Pythagoras theorem for right triangles, we have a triangle inequality theorem for acute triangles. It states that the sum of thesquares of the two sides of a triangle is greater than the square of the largest side. if the sides measure such that is thelargest side, then,
In other words, in a triangle, if the triangle is an acute triangle.
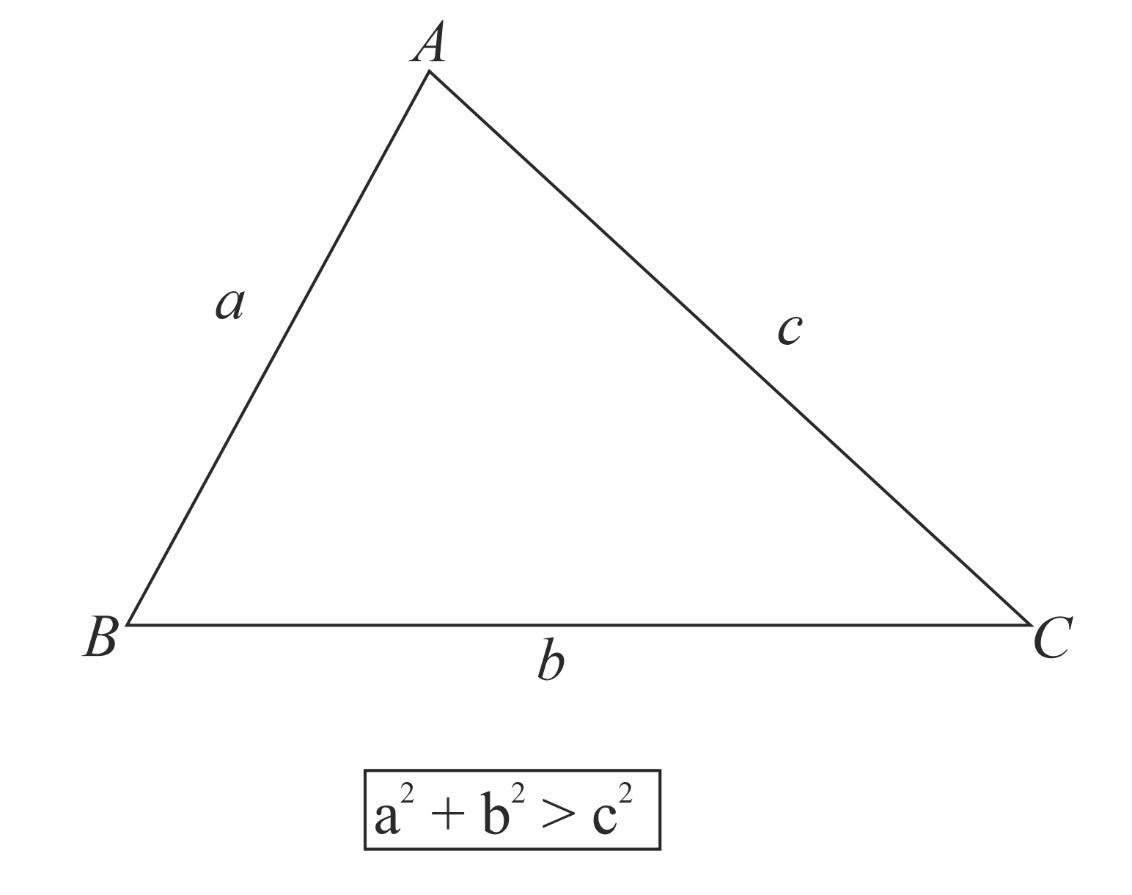
Obtuse Angled Triangle Theorem:
An obtuse-angled triangle or obtuse triangle is a type of triangle whose one of the vertex angles is larger than An obtuse-angled triangle has one of its vertex angles as obtuse and other angles as acute angles
i.e. if one of the angles measure more than then the sum of the other two angles is less than The side opposite to the obtuse angle is considered the longest. For example, in a triangle three sides of a
triangle measure and being the longest side of the triangle as it is the opposite side to the obtuse angle.
Hence, the triangle is an obtuse-angled triangle where
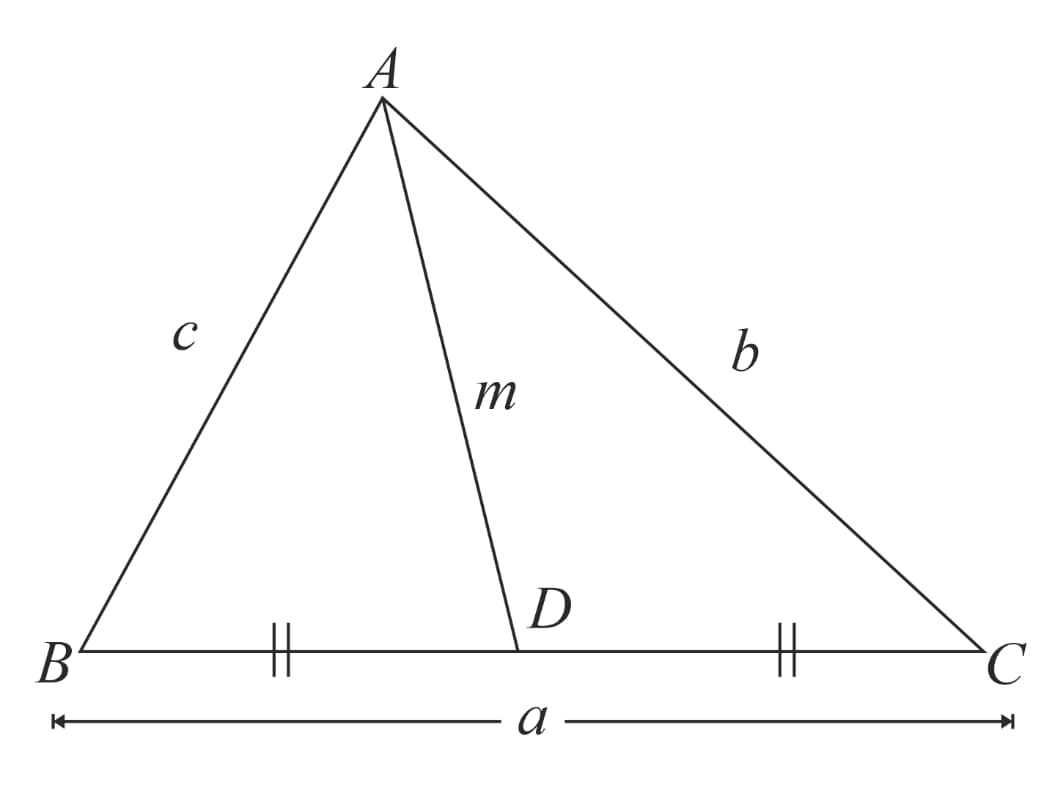
Apollonius Theorem:
In a triangle, the sum of squares of any two sides is equal to the sum of half the square of third side and twice the square of corresponding median.
Mathematically, if and are the sides of and is the length of corresponding median (as shown in the figure below), then
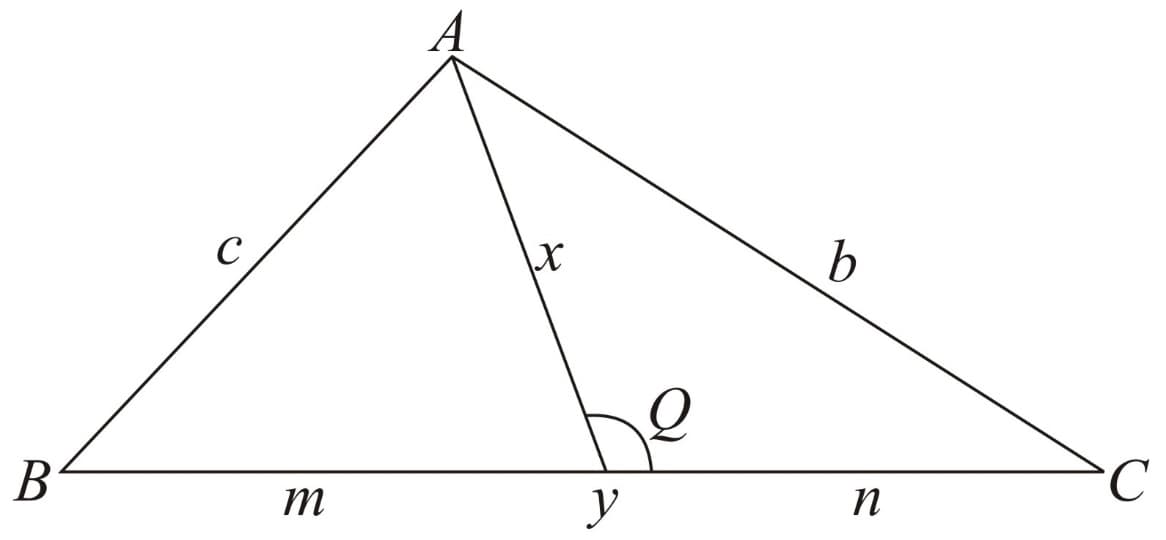
Stewart's Theorem:
Let and be the length of the sides of the triangle Let be the length of the cevian to the side of length a, If the cevian divides the side of length into two segments of length and with adjacent to and n adjacent to then Stewart's Theorem states that:
Trigonometric Form of Ceva's Theorem:
The theorem states that, in three Cevians and are concurrent iff the following identity holds:
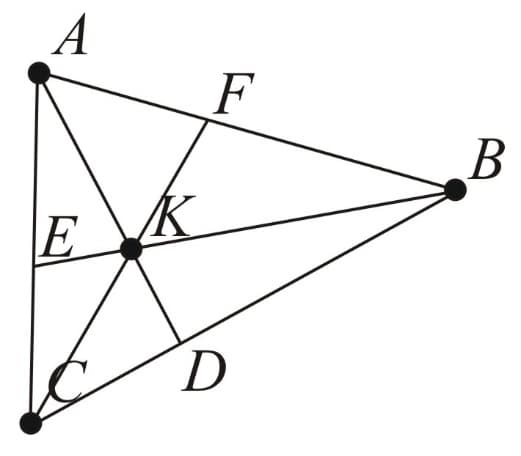
The theorem also has a trigonometric form
Or
The latter may serve as a source of great many trigonometric identities - some obvious, some much less so. Some unexpected identities can be obtained by placing the six points at the vertices of a regular polygon. If the Cevians are extended to intersect the circumscribed circle, they become three diagonals (or sides) of the regular polygon. We are of course concerned with the case where a regular polygon has three concurrent diagonals.
Converse of Ceva's Theorem: Given triangle with points on on and on such that
, then the cevians and are concurrent.
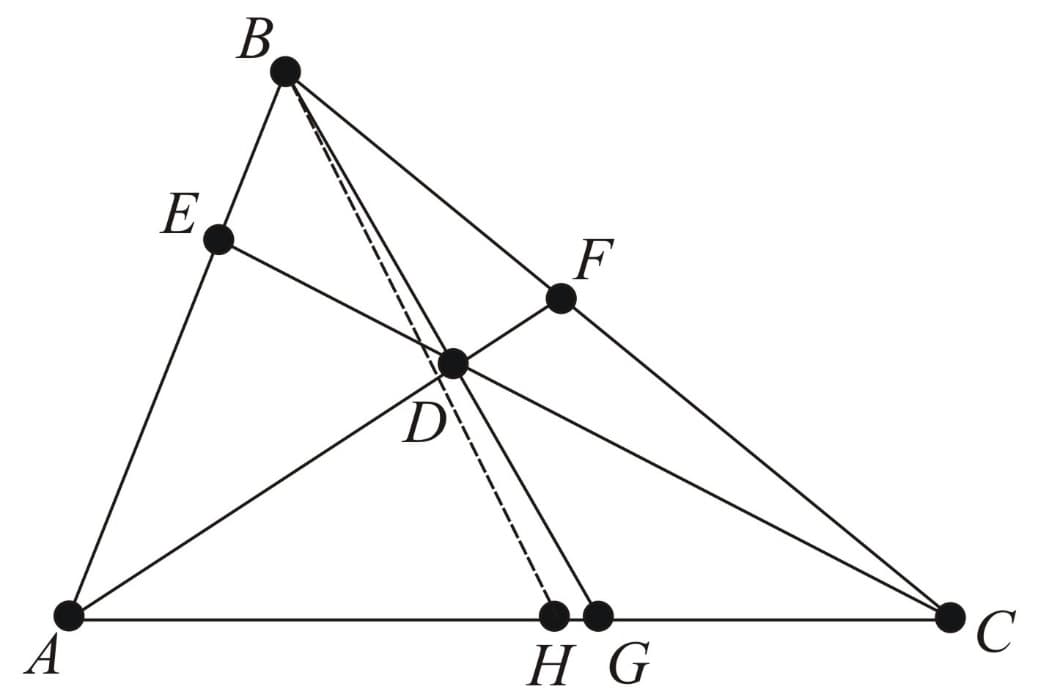
Nagel Point:
Given a triangle let and be the extouch points in which the -excircle meets line the excircle meets line and -excircle meets line respectively. The lines concur in the Nagel point of triangle
Menelaus' Theorem:
Menelaus' theorem relates ratios obtained by a line cutting the sides of a triangle. The converse of the theorem (i.e. three points on a triangle are collinear if and only if they satisfy certain criteria) is also true and is extremely
powerful in proving that three points are collinear.
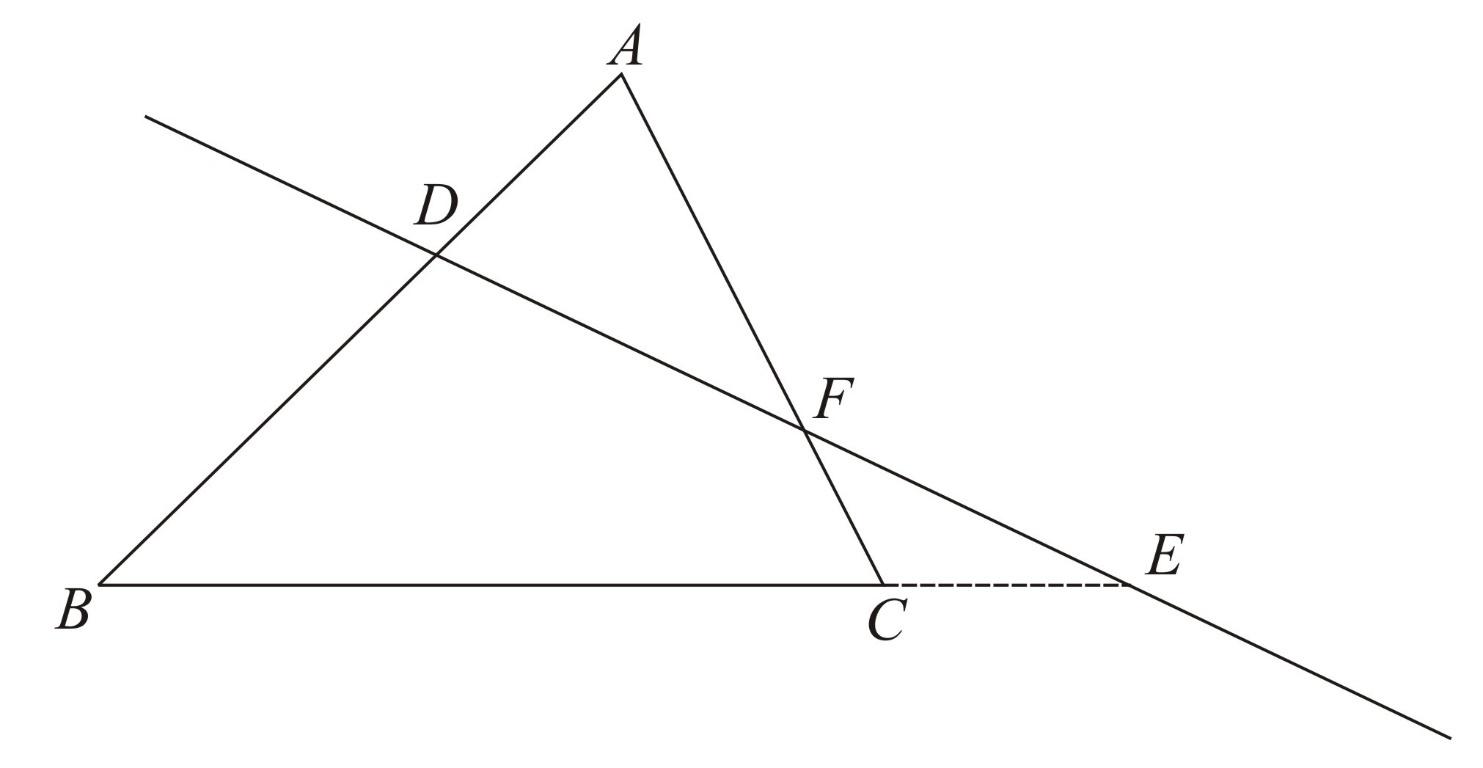
Collinear points on respectively
Menelaus' theorem states that if a line intersects or extended sides at points and the following statement holds:
Converse of Menelaus' Theorem: Suppose three points are on sides(or extension) respectively, such that or of them are in the extensions of the sides. Then points are collinear if and only if
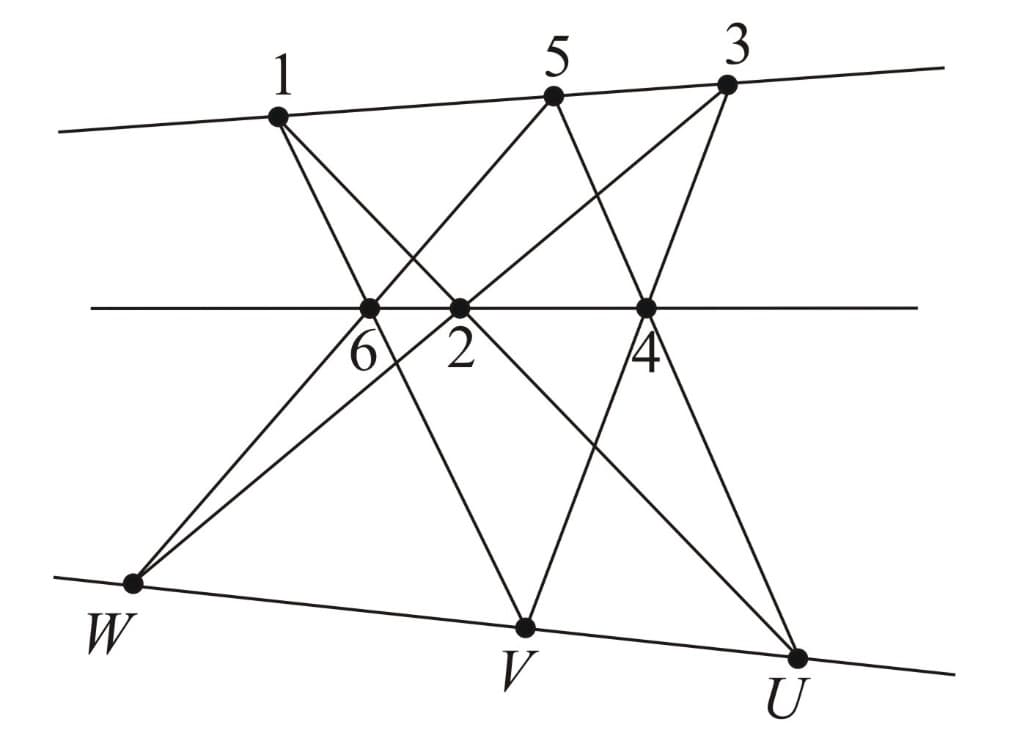
Pappus' Theorem:
This theorem states that if we take three points on a line, and another three points on another line, then the three intersection points of the following line pairs are collinear.
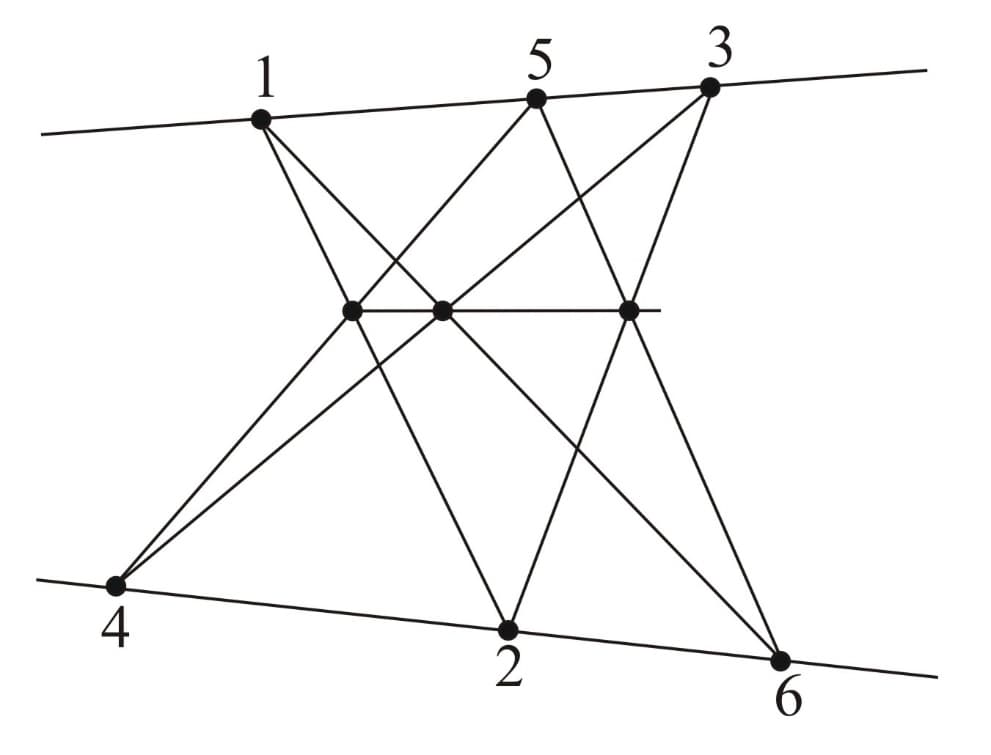
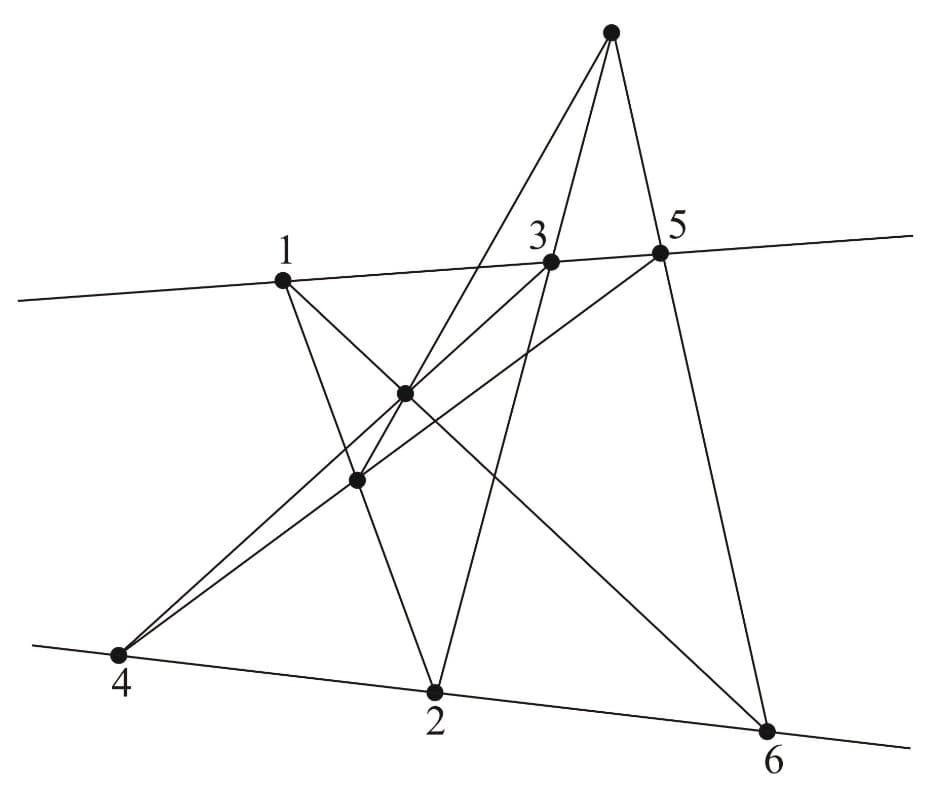
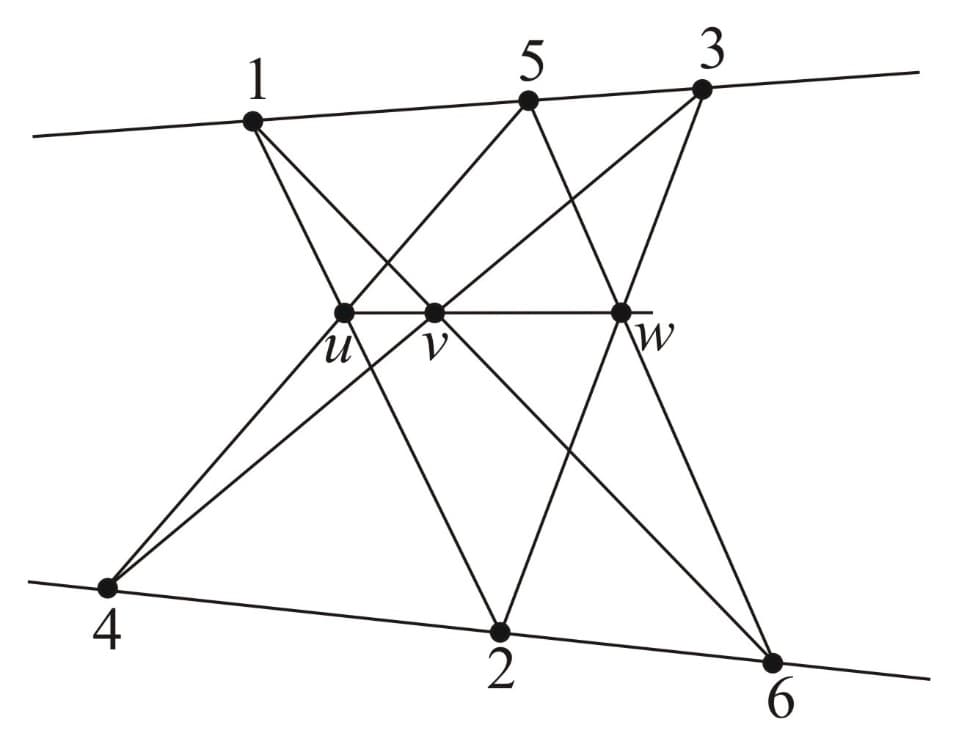
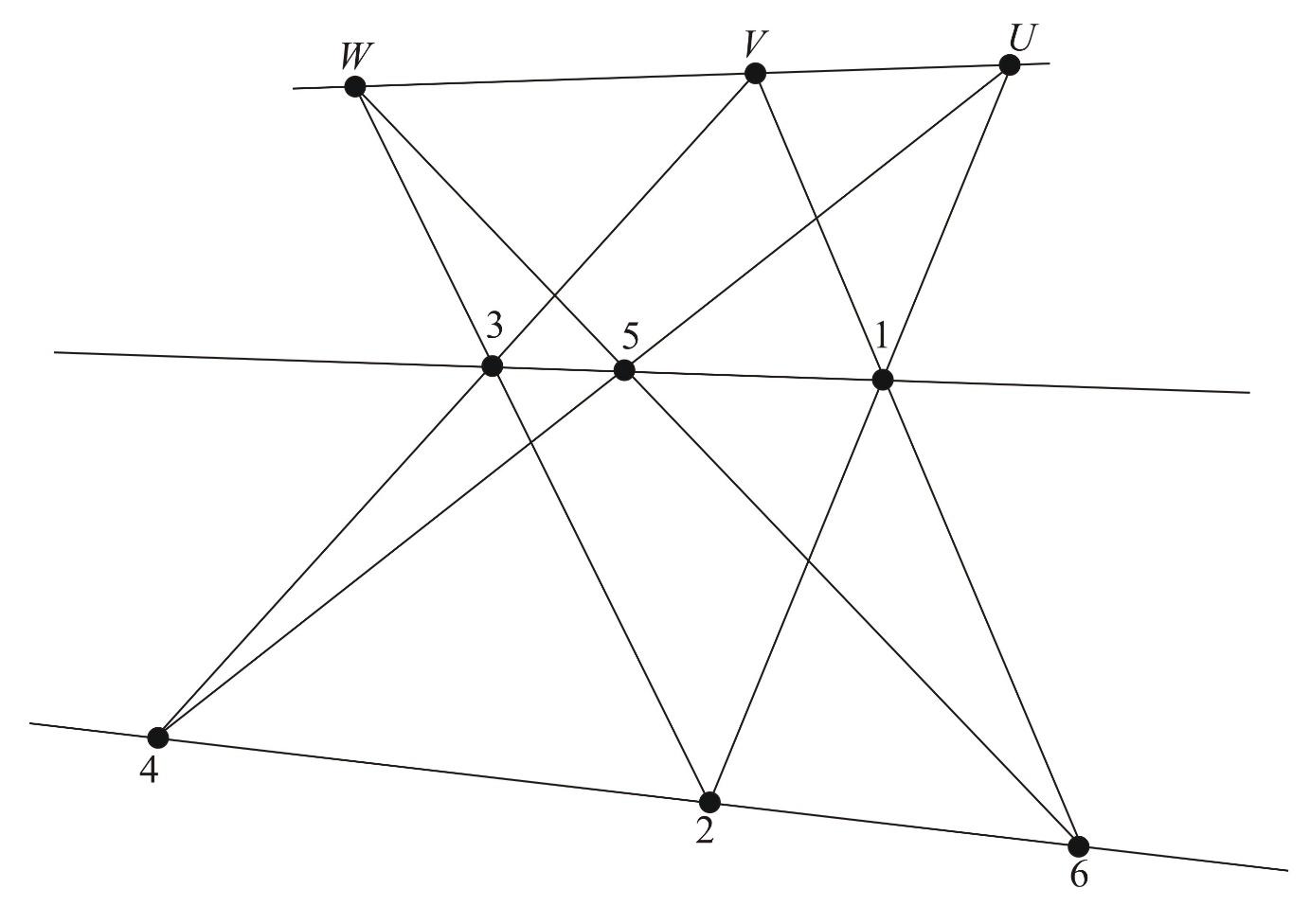
The figures below illustrate another interesting aspect of Pappus' theorem, that is the roles of the hexagon's vertices and the intersection points can be interchanged.
As we can see, in the second figure, the intersection points are interchanged with the vertices and in the last figure, the intersection points are swapped with
1. A quadrilateral is a closed figure obtained by joining four points (with no three points collinear) in an order.
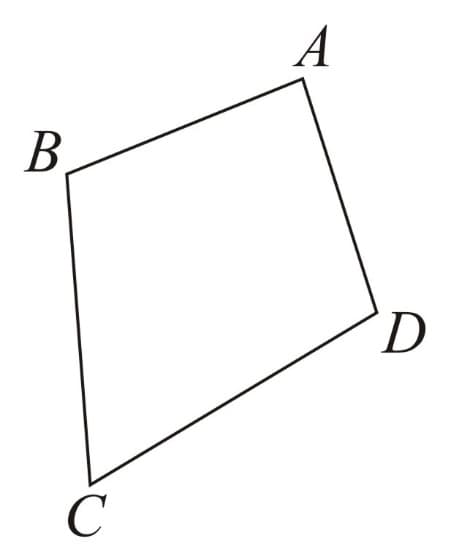
Here, is a quadrilateral.
2. A quadrilateral has four sides, four angles and four vertices.
3. Two sides of a quadrilateral having no common end point are called its opposite sides.
4. Two sides of a quadrilateral having a common end point are called its adjacent sides.
5. Two angles of a quadrilateral having common arm are called its adjacent angles.
6. Two angles of a quadrilateral not having a common arm are called its opposite angles.
7. A diagonal is a line segment obtained on joining the opposite vertices.
8. Sum of all the angles of a quadrilateral is This is known as the angle sum property of a quadrilateral.
9. Types of quadrilaterals and their properties:
| Name of quadrilateral | Properties |
|---|---|
|
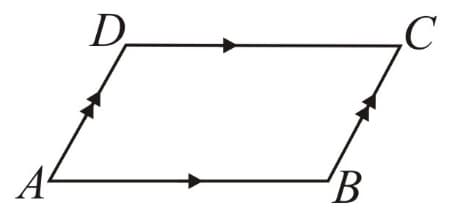
Parallelogram: A quadrilateral with each pair of opposite sides parallel.
|
i. Opposite sides are equal. ii. Opposite angles are equal. iii. Diagonals bisect one another. |
|
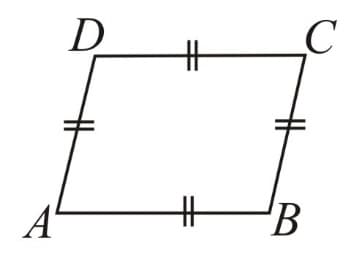
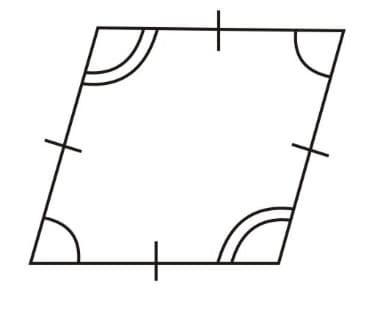
Rhombus: A parallelogram with sides of equal length.
|
i. All properties of a parallelogram. ii. Diagonals are perpendicular to each other. |
|
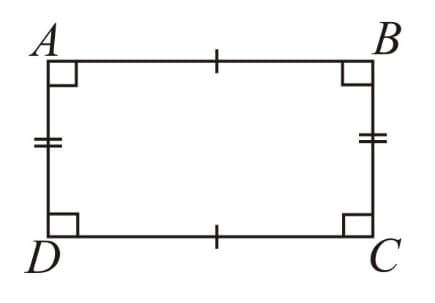
Rectangle: A parallelogram with a right angle.
|
i. All the properties of a parallelogram. ii. Each of the angles is a right angle. iii. Diagonals are equal. |
|
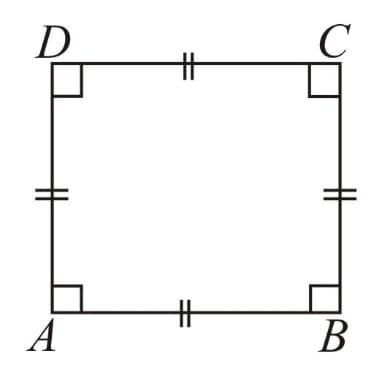
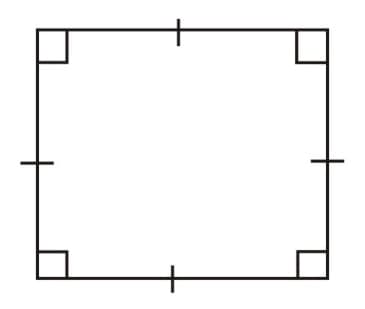
Square: A rectangle with sides of equal length.
|
All the properties of a parallelogram, a rhombus and a rectangle. |
|
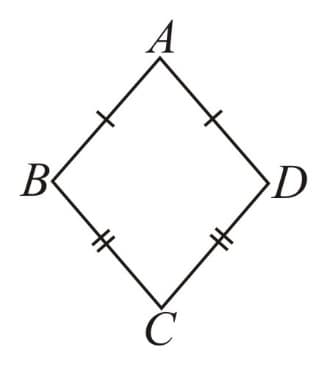
Kite: A quadrilateral with exactly two pairs of equal consecutive sides.
|
i. The diagonals are perpendicular to one another. ii. One of the diagonals bisects the other. iii. If is a kite, then but |
|
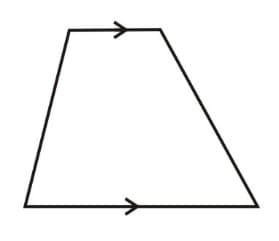
Trapezium: A quadrilateral with one pair of parallel side is called trapezium.
|
i. One pair of parallel sides. |
10. If the non-parallel sides of trapezium are equal, it is known as isosceles trapezium.
11. Square, rectangle and rhombus are all parallelograms.
12. Kite and trapezium are not parallelograms.
13. A square is a rectangle.
14. A square is a rhombus.
15. A parallelogram is a trapezium.
16. Properties of parallelogram:
i. The opposite sides of a parallelogram are parallel.
ii. A diagonal of a parallelogram divides it in two congruent triangles.
iii. The opposite sides of a parallelogram are equal.
iv. The opposite angles of a parallelogram are equal.
v. The consecutive angles (conjoined angles) of a parallelogram are supplementary.
vi. The diagonals of a parallelogram bisect each other.
17. A quadrilateral is a parallelogram if:
i. each pair of opposite sides of a quadrilateral is equal, or
ii. each pair of opposite angles is equal, or
iii. if the diagonals of a quadrilateral bisect other, or
iv. if a pair of opposite sides is equal and parallel.
Mid-point Theorem (varignon's Theorem):- The mid point of the sides of any arbitrary quadrilateral form a parallelogram. Also, the area of parallelogram will be half the area of quadrilateral.
| Quadrilateral formulas | Rectangle | Square | Parallelogram | Rhombus | Trapezium |
|---|---|---|---|---|---|
| Area | |||||
| Perimeter | Sum of all the sides |
Polygon Definition
A polygon is an enclosed shape with straight lines. -dimensional shapes like Rectangle, square etc are categorized under polygon. Polygons have a finite number of sides. A circle is not a polygon as it has a curved shape. The points where the straight lines meet are called vertices. The interior is called the body.
Types of Polygon
There are mainly types of Polygon:
1. Regular Polygon- The polygon which has equal sides and equal angles. Generally, questions from regular polygon are asked in the exam.
2. Irregular Polygon- The one with unequal sides and angles. Below figures show Regular and Irregular Polygons:
Properties of Polygon
- Polygon: It is a closed plane figure bounded by three or more than three straight lines.
- Regular Polygon: All the sides are equal and also all the interior angles are equal
Sum of Interior angles of a polygon
number of sides
Sum of exterior angle
Important Formulae Related to Regular Polygon :
The important Polygon formulas have been listed below including the formula for the area of a polygon.

(circumcircle radius)
Area
Regular Hexagon
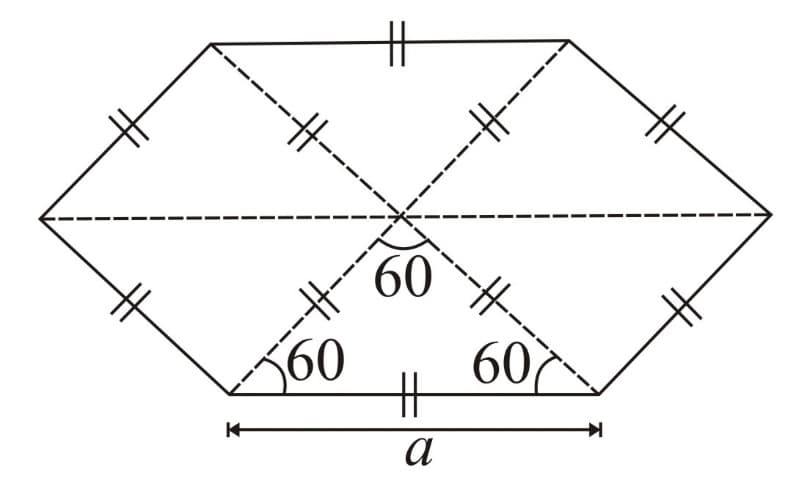
(Inradius)
(Circumradius)
Area
Regular Octagon
Area
Properties of Polvgon:-
Sum of all angle of an -sided Polygon is:-
Each angle of an Regular Polygon
Sum of All the Exterior Angles of a polygon
-Sided polygon has
| Types of Polygons | ||
|---|---|---|
|
Regular, convex
|
irregular, convex
|
irregular, concave
|
1. Definition:
(i) A circle is the collection of those points in a plane that are at a given constant distance from a given fixed-point in the plane. The fixed point is called the Centre and the given constant distance is called the Radius of the circle.
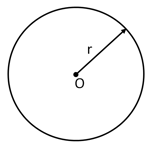
(ii) There is one and only one Circle passing through three given non-collinear points.
2. Terms Related to Circles:
(i) A point lies inside or on or outside the Circle according to as or or
(ii) The collection of all points lying inside and on the circle is called a Circular Disc with centre and radius
(iii) Circles having the same centre and different radii are said to be Concentric Circles.
(iv) Two circles are said to be congruent if either of them can be superposed on the other to cover it exactly.
(v) A continuous piece of a Circle is called an Arc of the Circle.
(vi) The length of an Arc is the length of the fine thread which just covers it completely.
(vii) Let be any circle. Then any angle whose vertex is is called the Central Angle.
(viii) An arc less than one half of the whole arc of a circle is called the Minor Arc of a Circle.
(ix) An arc greater than one half of the whole arc of a circle is called the Major Arc of a Circle.
(x) A line segment joining any two points on a circle is called a Chord of the circle.
3. Chord Properties of a Circle:
(i) A Chord passing through the centre of a circle is known as its diameter. A Diameter of a circle divides it into two equal parts which are arcs. Each of these two arcs is called a Semi-Circle.
(ii) If two arcs of a circle are congruent, then corresponding chords are equal.
(iii) If two Chords of a Circle are equal, then their corresponding Arcs are congruent.
(iv) The perpendicular from the Centre of a Circle to a Chord bisects the Chord.
(v) The line segment joining the Centre of a Circle to the mid-point of a Chord is perpendicular to the Chord.
(vi) If two circles intersect in two points, then the line through the centres is perpendicular to the common Chord.
(vii) Equal Chords of a circle are equidistant from the centre.
(viii) Chords of a circle which are equidistant from the centre are equal.
(ix) Of any two Chords of a circle, the larger Chord is nearer to the centre.
(x) Of any two Chords of a circle, the Chord nearer to the centre is larger.
4. Angle Properties of Arc and Chord of a Circle:
(i) Equal Chords of a Circle subtend equal angle at the Centre.
(ii) If the angles subtended by two Chords of a Circle at the centre are equal, the Chords are equal.
(iii) The angle subtended by an Arc of a Circle at the centre is double the angle subtended by it at any point on the remaining part of the Circle.
(iv) Angles in the same segment of a Circle are equal.
(v) The angle in a Semi-Circle is a right angle.
5. Concentric Circles:
Circles having the same centre and different radii are said to be concentric circles.
6. Congruent Circles:
Two circles are said to be congruent if either of them can be superposed on the other so as to cover it exactly.
7. Cyclic Quadrilateral:
(i) If all vertices of a quadrilateral lie on a circle, it is called a cyclic quadrilateral.
(ii) The opposite angles of a cyclic quadrilateral are supplementary.
(iii) If the sum of any pair of opposite angles of a quadrilateral is then it is cyclic.
(iv) If one side of a cyclic quadrilateral is produced, then the exterior angle is equal to the interior opposite angle.
(v) An isosceles trapezium is cyclic.
8. Tangent of a Circle:
(i) A tangent to a circle is a line that intersects the circle at only one point.
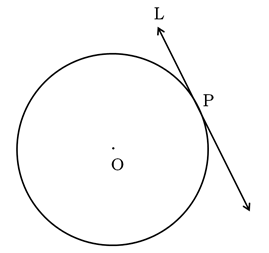
(ii) Tangent to a circle at a point is perpendicular to the radius through the point of contact.
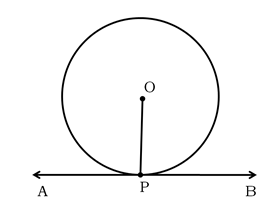
(iii) The tangent to a circle is a special case of the secant, when the two end points of its corresponding chord coincide.
9. Number of Tangents to a Circle:
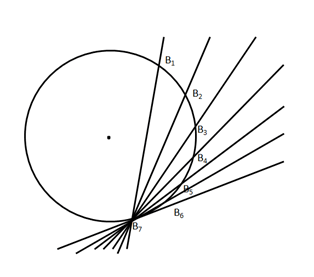
(i) From a point on the circle only one tangent can be drawn.
(ii) From a point, lying outside a circle, two and only two tangents can be drawn to it.
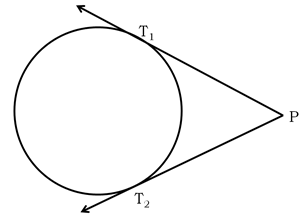
(iii) The lengths of the two tangents drawn from an external point to a circle are equal.
10. Secant:
A secant is a line which intersects the circle at two distinct points and the line segment between the points is a chord.
11. Area of Segment:
Area of segment of a circle Area of the corresponding sector Area of the corresponding triangle.
12. Sector of a Circle
The region enclosed by two radii and an arc of a circle is called the sector of a circle. Any radius divides the circle into two sectors. The region enclosed by the major arc and radius of the circle is the major sector and, the region formed by the minor arc and the radius of the circle is the minor sector.
13. Circumcircle
The circumcircle of a triangle or other polygon is the circle which passes through all of its vertices. Every triangle has only one circumcircle. Those quadrilaterals with circumcircles form cyclic quadrilaterals.
The center of the circumcircle is known as the circumcenter. It is the intersection point of the perpendicular bisectors of the edges of the polygon.
The radius of the circumcircle is known as the circumradius.
14. The Pitot Theorem
The theorem states that in a tangential quadrilateral the two sums of lengths of opposite sides are the same.
The converse is also true: a circle can be inscribed into every convex quadrilateral in which the lengths of opposite sides sum to the same value.
i.e. if a quadrilateral is tangential to or circumscribed around a circle, then the two sums of opposite sides are equal, i.e. .
15. Miquel's Theorem
Miquel's Theorem is named after Auguste Miquel. If we draw any triangle, pick a point on each side, and connect these in pairs to the vertices using circles then the circles will always intersect in a single point, called the Miquel point.
16. Pivot theorem
The pivot theorem states that, given any three points and on each side of a triangle , the three circles through the points and share a common point. Conversely: given any three circles sharing a common point, there are an infinite number of triangles such that one point lies on each circle and the sides of the triangle pass through the intersection points of the circles.