EASY

Earn 100

What are the condition for node and antinode?

Important Questions on Superposition of Waves

HARD

Physics>Waves and Oscillations>Superposition of Waves>Formation of Stationary Waves on String

A horizontal stretched string, fixed at two ends, is vibrating in its fifth harmonic according to the equation,

y (x, t) = (0 .01 m) sin [(62.8 m^{-1}) x] cos [(628 s^{-1}) t]

. Assuming

π = 3.14

, the correct statement(s) is (are):

HARD

Physics>Waves and Oscillations>Superposition of Waves>Formation of Stationary Waves on String

A stretched sonometer wire is in unison with a tuning fork. When the length of the wire is increased by 5%, the number of beats heard per second is 10. Find the frequency of the tuning fork.

EASY

Physics>Waves and Oscillations>Superposition of Waves>Formation of Stationary Waves on String

A wire of density

9 \times 10^{- 3} kg {cm}^{- 3}

is stretched between two clamps

1 m

apart. The resulting strain in the wire is

4.9 \times 10^{- 4}

. The lowest frequency of the transverse vibrations in the wire (Young's modulus of wire

Y = 9 \times 10^{10} {Nm}^{- 2}

), (to the nearest integer),_______

MEDIUM

Physics>Waves and Oscillations>Superposition of Waves>Formation of Stationary Waves on String

The maximum amplitude of the resultant wave due to the linear superposition of two waves

y_{1} (x, t) = A s i n (k x - ω t)

and

y_{2} (x, t) = A s i n (k x + ω t)

, occurs at

x

values

EASY

Physics>Waves and Oscillations>Superposition of Waves>Formation of Stationary Waves on String

Two identical wires are vibrating in unison. If the tension in one of the wires is increased by

2 %

, five beats are produced per second by the two vibrating wires. The initial frequency of each wire is

(\sqrt{1.02} = 1.01)

EASY

Physics>Waves and Oscillations>Superposition of Waves>Formation of Stationary Waves on String

The equation of a stationary wave is

y = 2 \sin (\frac{π x}{15}) \cos (48 π t)

. The distance between a node and its next antinode is

HARD

Physics>Waves and Oscillations>Superposition of Waves>Formation of Stationary Waves on String

In Melde’s experiment, when tension in the string is

10 g

wt then three loops are obtained. Determine the tension in the string required to obtain four loops, if all other conditions are constant.

HARD

Physics>Waves and Oscillations>Superposition of Waves>Formation of Stationary Waves on String

Two uniform wires of the same material are vibrating under the same tension. If the first overtone of the first wire is equal to the second overtone of the second wire and radius of the first wire is twice the radius of the second wire then the ratio of the lengths of the first wire to second wire is

HARD

Physics>Waves and Oscillations>Superposition of Waves>Formation of Stationary Waves on String

The ratio of the fundamental frequencies of two identical strings after one of them was stretched by

2 %

and the other by

4 %

is (Assume that the tension is proportional to the elongation)

HARD

Physics>Waves and Oscillations>Superposition of Waves>Formation of Stationary Waves on String

In stationary wave, the distance between a node and its adjacent anti-node is____.

EASY

Physics>Waves and Oscillations>Superposition of Waves>Formation of Stationary Waves on String

A string fixed at both ends vibrates in $5$ loops as shown in the figure. The total number of nodes and antinodes respectively are

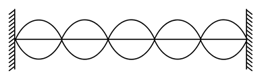
Question Image

EASY

Physics>Waves and Oscillations>Superposition of Waves>Formation of Stationary Waves on String

A standing wave is formed by the superposition of two waves travelling in opposite directions. The transverse displacement is given by,

y (x, t) = 0.5 \sin (\frac{5 π}{4} x) \cos (200 π t)

. What is the speed of the travelling wave moving in the positive

x

direction? (

x

and

t

are in meter and second, respectively)

MEDIUM

Physics>Waves and Oscillations>Superposition of Waves>Formation of Stationary Waves on String

The equation of the stationary wave along a stretched string is given by

$y = 5 \sin \frac{π x}{3} \cos 40 π t$

where $x$ and $y$ are in $cm$ and $t$ in $s$ . The separation between two adjacent nodes is

EASY

Physics>Waves and Oscillations>Superposition of Waves>Formation of Stationary Waves on String

A string is vibrating in its fifth overtone between two rigid supports

2.4 m

apart. The distance between successive node and antinode is

MEDIUM

Physics>Waves and Oscillations>Superposition of Waves>Formation of Stationary Waves on String

Two travelling waves produces a standing wave represented by equation.

y = (1.0 mm) \cos [(1.57 {cm}^{- 1}) x] \sin [(78.5 s^{- 1}) t]

. The node closest to the origin in the region

x > 0

will be at

x = . . . . . . (in cm) .

MEDIUM

Physics>Waves and Oscillations>Superposition of Waves>Formation of Stationary Waves on String

When a string is divided into three segments of lengths $l_{1}, l_{2} and l_{3}$ the fundamental frequencies of these three segments are $ν_{1}, ν_{2} and ν_{3}$ respectively. The original fundamental frequency $ν$ of the string is

MEDIUM

Physics>Waves and Oscillations>Superposition of Waves>Formation of Stationary Waves on String

Two strings of the same material and same length are given equal tension. If they are vibrating with fundamental frequencies

1600 Hz

and

900 Hz,

then the ratio of their respective diameters is

MEDIUM

Physics>Waves and Oscillations>Superposition of Waves>Formation of Stationary Waves on String

A standing wave is produced on a string fixed at one end and free at other. The length of string must be an _______.

EASY

Physics>Waves and Oscillations>Superposition of Waves>Formation of Stationary Waves on String

A standing wave pattern can be represented by an equation like

HARD

Physics>Waves and Oscillations>Superposition of Waves>Formation of Stationary Waves on String

One end of a taut string of length 3m along the x axis is fixed at x = 0. The speed of the waves in the string is

100 m s^{- 1}

. The other end of the string is vibrating in the y direction so that stationary waves are set up in the string. The possible waveform(s) of these stationary waves is (are)

What are the condition for node and antinode?

Important Questions on Superposition of Waves

Learn and Prepare for any exam you want !