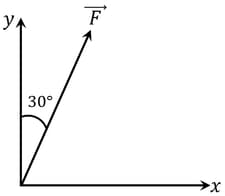
What are the rectangular components of a vector ?
Important Questions on Vectors, Scalars and Elementary Calculus
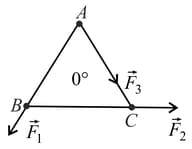
Figure shows three forces and acting along the sides of an equilateral triangle. If the total torque acting at point (centre of the triangle) is zero then the magnitude of is
If y-component of a force acting in x-y plane is . Then the x- component will be
Consider a frame that is made up of two thin massless rods and as shown in the figure. A vertical force of magnitude is applied at point of the frame.
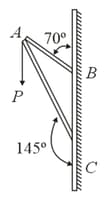
Suppose the force is resolved parallel to the arms and of the frame. The magnitude of the resolved component along the arm is . The value of , to the nearest integer, is ________.
[Given : ]
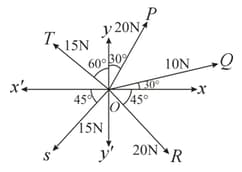
In an octagon of equal side, what is the sum of if,
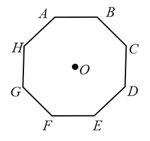
The resultant of these forces and is approximately ______
[Take Given and unit vectors along axis]