EASY
Earn 100
What is a point?
Important Questions on Introduction to Euclid's Geometry
EASY
In the adjoining figure, name :
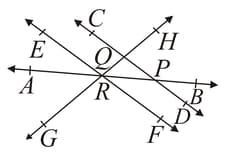
Three concurrent lines and their points of intersection.
EASY
EASY
In the adjoining figure, name :
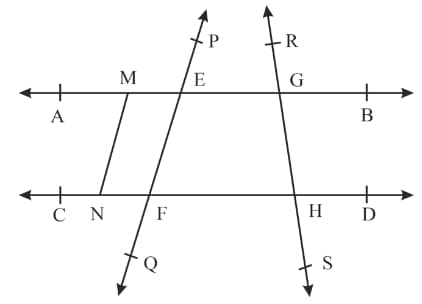
Six Points
EASY
A line has a definite length.
EASY
( ) Two lines in a plane not having any point common are called P lines.
( ) The edges of a surface are Q .
( ) Two distinct planes can intersect at R points.
( ) S planes can pass through two distinct points.
P Q R S
(A) Parallel lines Infinite infinite
(B) Parallel planes one one
(C) Perpendicular lines one zero
(D) Perpendicular planes infinite infinite
EASY
EASY
A line is the same as line .
EASY
The side faces of a pyramid are
MEDIUM
( ) ‘There are infinite points on a line’ is an Euclidean postulate.
( ) Only one plane passes through three non-collinear points.
( ) Boundaries of solids are surfaces.
(i) (ii) (iii)
(A) F F F
(B) T T F
(C) T F T
(D) F T T
EASY
Consider two ‘postulates' given below:
(i) Given any two distinct point and , there exists a third point which is in between and .
(ii) There exist at least three points that are not on the same line.
Do these postulates contain any undefined terms? Are these postulates consistent? Do they follow from Euclid postulates? Explain.
EASY
In the adjoining figure, name :
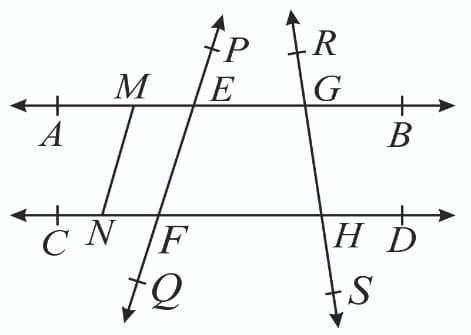
Four lines
MEDIUM
EASY
EASY
In the adjoining figure, name :
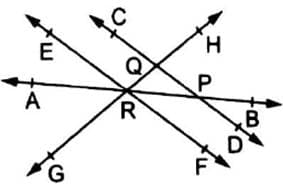
Three rays
EASY
From the given figure, name three lines.
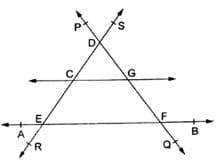
EASY
EASY
Boundaries of surfaces are
EASY
Which of the following is a true statement?
EASY
EASY

