EASY

Earn 100

What is significance of Young's modulus of elasticity?

Important Questions on Properties of Solids and Liquids

EASY

Physics>Physical and Thermal Properties of Bulk Matter>Properties of Solids and Liquids>Stress Strain Relationship

For a perfectly rigid body,

MEDIUM

Physics>Physical and Thermal Properties of Bulk Matter>Properties of Solids and Liquids>Stress Strain Relationship

A load of mass

M kg

is suspended from a steel wire of length

2 m

and radius

1.0 mm

in Searle's apparatus experiment. The increase in length produced in the wire is

4.0 mm .

Now the load is fully immersed in a liquid of relative density

2 .

The relative density of the material of load is

8 .

The new value of increase in length of the steel wire is:

EASY

Physics>Physical and Thermal Properties of Bulk Matter>Properties of Solids and Liquids>Stress Strain Relationship

Copper of fixed volume

V

is drawn into wire of length

l

. When this wire is subjected to a constant force

F,

the extension produced in the wire is

∆ l .

Which of the following graph is a straight line?

MEDIUM

Physics>Physical and Thermal Properties of Bulk Matter>Properties of Solids and Liquids>Stress Strain Relationship

The Young's modulus of steel is twice that of brass. Two wires of same length and of same area of cross-section, one of steel and another of brass are suspended from the same roof. If we want the lower ends of the wires to be at the same level, then the weights added to the steel and brass wires must be in the ratio of:

EASY

Physics>Physical and Thermal Properties of Bulk Matter>Properties of Solids and Liquids>Stress Strain Relationship

A rubber cord of density

d,

Young's modulus

Y

and length

L

is suspended vertically. If the cord extends by a length

0.5 L

under its own weight, then

L

EASY

Physics>Physical and Thermal Properties of Bulk Matter>Properties of Solids and Liquids>Stress Strain Relationship

A metallic rod breaks when strain produced is

0.2 %

. Young's modulus of the material of the rod is

7 \times 10^{9} N m^{- 2}

. What should be its area of cross-section to support a load of

10^{4} N

MEDIUM

Physics>Physical and Thermal Properties of Bulk Matter>Properties of Solids and Liquids>Stress Strain Relationship

Young's moduli of two wires

A

and

B

are in the ratio

7 : 4

. Wire

A

2 m

long and has radius

R .

Wire

B

1.5 m

long and has radius

2 m m .

If the two wires stretch by the same length for a given load, the value of

R

is close to:

MEDIUM

Physics>Physical and Thermal Properties of Bulk Matter>Properties of Solids and Liquids>Stress Strain Relationship

A rubber cord has a cross-sectional area

10^{- 6} m^{2}

and total unstretched length

0.1 m

. It is stretched to

0.125 m

and then released to project a particle of mass

5.0 g

. The velocity of projection is [Given, Young's modulus of rubber,

Y = 5 \times 10^{8} N m^{- 2}

]

MEDIUM

Physics>Physical and Thermal Properties of Bulk Matter>Properties of Solids and Liquids>Stress Strain Relationship

A steel rail of length

5 m

and area of cross section

40 {cm}^{2}

is prevented from expanding along its length while the temperature rises by

10 ° C

. If coefficient of linear expansion and Young's modulus of steel are

1.2 \times 10^{- 5} K^{- 1}

and

2 \times 10^{11} N m^{- 2}

respectively, the force developed in the rail is approximately:

HARD

Physics>Physical and Thermal Properties of Bulk Matter>Properties of Solids and Liquids>Stress Strain Relationship

A uniformly tapering conical wire is made from a material of Young's modulus

Y

and has a normal, unextended length

L

. The radii, at the upper and lower ends of this conical wire, have values

R

and

3 R

, respectively. The upper end of the wire is fixed to a rigid support and a mass

M

is suspended from its lower end. The equilibrium extended length, of this wire, would equal:

EASY

Physics>Physical and Thermal Properties of Bulk Matter>Properties of Solids and Liquids>Stress Strain Relationship

An object of mass

m

is suspended at the end of a massless wire of length

L

and area of cross-section, A. Young modulus of the material of the wire is

Y

. If the mass is pulled down slightly its frequency of oscillation along the vertical direction is :

HARD

Physics>Physical and Thermal Properties of Bulk Matter>Properties of Solids and Liquids>Stress Strain Relationship

A pendulum made of a uniform wire of cross sectional area A has time period T. When an additional mass M is added to its bob, the time period changes to

T_{M}

. If the Young's modulus of the material of the wire is

Y

, then

\frac{1}{Y}

is equal to:
(

g =

gravitational acceleration)

EASY

Physics>Physical and Thermal Properties of Bulk Matter>Properties of Solids and Liquids>Stress Strain Relationship

A wire of length

L

, area of cross section

A

is hanging from a fixed support. The length of the wire changes to

L_{1}

when mass

M

is suspended from its free end. The expression for Young’s modulus is:

MEDIUM

Physics>Physical and Thermal Properties of Bulk Matter>Properties of Solids and Liquids>Stress Strain Relationship

Three thin wires of equal length are suspended from the top of a roof. The respective ratio of their area of cross section is

1 : 2 : 4

and Young's modulii is

4 : 2 : 1,

then the ratio of their weights to be attached at the other ends to obtain same elongation in them is

EASY

Physics>Physical and Thermal Properties of Bulk Matter>Properties of Solids and Liquids>Stress Strain Relationship

The Young's modulus of a perfectly rigid body is

HARD

Physics>Physical and Thermal Properties of Bulk Matter>Properties of Solids and Liquids>Stress Strain Relationship

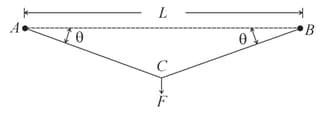
String $A B$ of unstretched length $L$ is stretched by applying a force $F$ at the mid-point $C$ such that the segments $A C$ and $B C$ make an angle $θ$ with $A B$ as shown in the figure. The string may be considered as an elastic element with a force to elongation ratio $K$ . The force $F$ is given by

Question Image

MEDIUM

Physics>Physical and Thermal Properties of Bulk Matter>Properties of Solids and Liquids>Stress Strain Relationship

A copper wire of cross-sectional area

0.01 {cm}^{2}

is under a tension of

22 N

. Find the percentage change in the cross-sectional area (Young's modulus of copper

= 1.1 \times 10^{11} N m^{- 2}

and Poisson ratio

= 0.32

)

HARD

Physics>Physical and Thermal Properties of Bulk Matter>Properties of Solids and Liquids>Stress Strain Relationship

A thin

1 m

long rod has a radius of

5 mm

. A force of

50 {π×10}^{3} N

is applied at one end to determine its Young's modulus. Assume that the force is exactly known. If the least count in the measurement of all lengths is

0.01 mm

, which of the following statements is false?

MEDIUM

Physics>Physical and Thermal Properties of Bulk Matter>Properties of Solids and Liquids>Stress Strain Relationship

A metal rod of length

L

and cross-sectional area

A

is heated through

T ° C

. What is the force required to prevent the expansion of the rod lengthwise?

[Y

= Young's modulus of the material of rod,

α =

coefficient of linear expansion

]

HARD

Physics>Physical and Thermal Properties of Bulk Matter>Properties of Solids and Liquids>Stress Strain Relationship

A steel wire of diameter

0.5 mm

and Young's modulus

2 \times 10^{11} N m^{- 2}

carries a load of mass

M

. The length of the wire with the load is

1.0 m

. A vernier scale with

10

divisions is attached to the end of this wire. Next to the steel wire is a reference wire to which a main scale, of least count

1.0 mm

, is attached. The 10 divisions of the vernier scale correspond to 9 divisions of the main scale. Initially, the zero of vernier scale coincides with the zero of main scale. If the load on the steel wire is increased by

1.2 kg

, the vernier scale division which coincides with a main scale division is __________. Take

g = 10 m s^{- 2} and π = 3.2

What is significance of Young's modulus of elasticity?

Important Questions on Properties of Solids and Liquids

Learn and Prepare for any exam you want !