What is the ratio of the total kinetic energy and the translational kinetic energy of a rolling body of radius $R$ and the radius of gyration $k$?

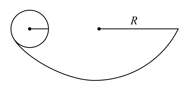
A solid sphere of mass $m$ and radius $r$ is released from rest from the given position. If it rolls without sliding on the circular track of radius $R$, its speed when it reaches its lowest position will be

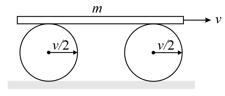
A plate of mass $m$ is placed on a solid and a hollow spheres, each of mass $m$. If the speed of the plate is $v$, assuming pure rolling of the spheres with all the contacting surfaces, the kinetic energy of the system (Spheres $+$ Plate) will be

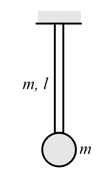
A particle is attached to the lower end of a uniform rod which is hinged at its other end, as shown in the figure. The minimum speed given to the particle, so that the rod performs circular motion in a vertical plane, will be [length of the rod is $l$. Consider the masses of both rod and particle to be the same]

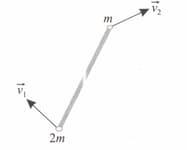
Two particles of masses $2m$ and $m$, interconnected by a uniform rigid rod of mass $m$, move with velocities $\overrightarrow{v_1}$ and $\overrightarrow{v_2}$, respectively. Find the momentum of the system $\left(m+\mathrm{rod}+2m\right)$.

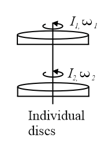
Two discs of the moment of inertias $I_1$ and $I_2$ about their respective axes (normal to the disc and passing through the centre), and rotating with angular speeds ${\mathrm{\omega }}_1$ and ${\mathrm{\omega }}_2$ are brought into contact face to face with their axes of the rotation coincident.

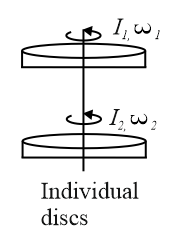
Does the law of conservation of angular momentum apply to the situation? Why?

Two discs of the moment of inertia $I_1$ and $I_2$ about their respective axes (normal to the disc and passing through the centre), and rotating with angular speeds ${\mathrm{\omega }}_1$ and ${\mathrm{\omega }}_2$ are brought into contact face to face with their axes of rotation coincident.

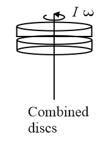
Find the angular speed of the two-disc system.

Two discs of moment of inertia $I_1$ and $I_2$ about their respective axes (normal to the disc and passing through the centre), and rotating with angular speeds ${\mathrm{\omega }}_1$ and ${\mathrm{\omega }}_2$ are brought into contact face to face with their axes of rotation coincident.

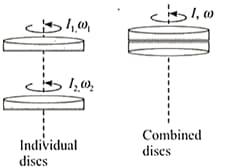
Calculate the loss in kinetic energy of the system in the process.

Two discs of the moment of inertias $I_1$ and $I_2$ about their respective axes (normal to the disc and passing through the centre), and rotating with angular speeds ${\mathrm{\omega }}_1$ and ${\mathrm{\omega }}_2$ are brought into contact face to face with their axes of rotation coincident.

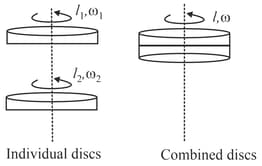
As a result, the energy of the system decreases. Which force is responsible for this loss in energy?