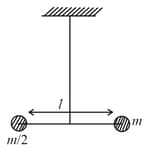
EASY
Earn 100
What is the time period of a second pendulum?
(Write the numerical value in terms of SI unit of time).
50% studentsanswered this correctly
Important Questions on Oscillations
MEDIUM
EASY
HARD
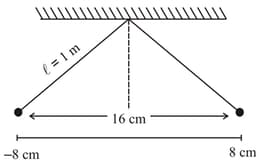
HARD
HARD
EASY
A simple pendulum has time period . The point of suspension is now moved upward according to the relation where is the vertical displacement. The time
period now becomes .
The ratio of is
MEDIUM
EASY
EASY
MEDIUM
MEDIUM
MEDIUM
EASY
Given below are two statements:
Statement : A second's pendulum has a time period of second.
Statement : It takes precisely one second to move between the two extreme positions. In the light of the above statements,
choose the correct answer from the options given below
EASY
EASY
EASY
EASY
HARD
EASY
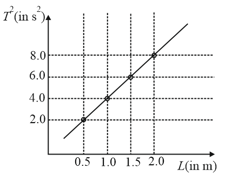
In an experiment to determine the gravitational acceleration of a place with the help of a simple pendulum, the measured time period squared is plotted against the string length of the pendulum in the figure. What is the value of at the place?
HARD