EASY

Earn 100

What is the total energy in simple harmonic motion at the mean position ?

Important Questions on Oscillations

EASY

Physics>Waves and Oscillations>Oscillations>Energy of a Particle Performing S.H.M

The variation of displacement with time of a particle executing free simple harmonic motion is shown in the figure.

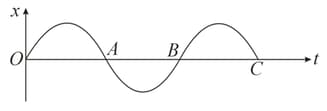
Question Image

The potential energy $U (x)$ versus time $(t)$ plot of the particle is correctly shown in figure:

MEDIUM

Physics>Waves and Oscillations>Oscillations>Energy of a Particle Performing S.H.M

A particle is executing simple harmonic motion

(S H M)

of amplitude

A,

along the

x

-axis, about

x = 0 .

When its potential Energy

(P E)

equals kinetic energy

(K E),

the position of the particle will be:

MEDIUM

Physics>Waves and Oscillations>Oscillations>Energy of a Particle Performing S.H.M

A particle of mass

1 kg

is hanging from a spring of force constant

100 N m^{- 1} .

The mass is pulled slightly downward and released so that it executes free simple harmonic motion with time period

T .

The minimum time when the kinetic energy and potential energy of the system will become equal, is

\frac{T}{n} .

The value of

n

is ________.

EASY

Physics>Waves and Oscillations>Oscillations>Energy of a Particle Performing S.H.M

A spring balance is loaded with two blocks

m_{1}

and

m_{2} .

where

m_{1}

is rigidly fixed with the spring and

m_{2}

is just kept over block

m_{1} .

The maximum energy of oscillation possible, assuming both the blocks are always in contact with each other, is

EASY

Physics>Waves and Oscillations>Oscillations>Energy of a Particle Performing S.H.M

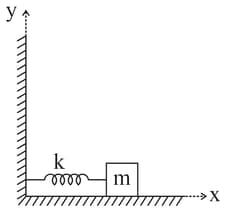
An object of mass $4 kg$ is attached to a spring which is fixed at one end on a rigid support and the mass-spring system is kept on a frictionless table. The object is allowed to execute simple harmonic motion along $X$ - direction. The force constant of the spring is $10 N m^{- 1}$ and the spring is stretched initially a distance of $5 cm$ , the total energy stored in the system is

Question Image

HARD

Physics>Waves and Oscillations>Oscillations>Energy of a Particle Performing S.H.M

A body of mass

1 kg

is executing simple harmonic motion (SHM). Its displacement

y

(in

cm

) at time t given by

y = [6 \sin (100 t + \frac{π}{4})] cm .

Its maximum kinetic energy is

EASY

Physics>Waves and Oscillations>Oscillations>Energy of a Particle Performing S.H.M

Total energy of a particle of mass '

m

' executing SHM given by

y = A \sin ω t

for any displacement is:

EASY

Physics>Waves and Oscillations>Oscillations>Energy of a Particle Performing S.H.M

x

is the displacement of the particle from the mean position, the total energy of a particle executing simple harmonic motion is

HARD

Physics>Waves and Oscillations>Oscillations>Energy of a Particle Performing S.H.M

An object of mass

0.5 kg

is executing simple harmonic motion. It amplitude is

5 cm

and time period (T) is

0.2 s

. What will be the potential energy of the object at an instant

t = \frac{T}{4} s

starting from mean position. Assume that the initial phase of the oscillation is zero.

HARD

Physics>Waves and Oscillations>Oscillations>Energy of a Particle Performing S.H.M

In a simple harmonic oscillation, what fraction of total mechanical energy is in the form of kinetic energy, when the particle is midway between mean and extreme position.

HARD

Physics>Waves and Oscillations>Oscillations>Energy of a Particle Performing S.H.M

The displacement of a particle in simple harmonic motion (SHM) is given by

y = \sqrt{3 π} \sin (\frac{100}{π} t + \frac{π}{4}) .

What will be the displacement of the particle from the mean position when its kinetic energy is eight times that of its potential energy?

EASY

Physics>Waves and Oscillations>Oscillations>Energy of a Particle Performing S.H.M

A body is executing S.H.M. Its potential energy is

E_{1}

and

E_{2}

at displacements

x

and

y

respectively. The potential energy at displacement

(x + y)

MEDIUM

Physics>Waves and Oscillations>Oscillations>Energy of a Particle Performing S.H.M

Obtain an expression for potential energy of a particle performing S.H.M. What is the value of potential energy at (i) Mean position and (ii) Extreme position.

EASY

Physics>Waves and Oscillations>Oscillations>Energy of a Particle Performing S.H.M

A particle executing simple harmonic motion along a straight line with an amplitude

A

, attains maximum potential energy when its displacement from mean position equals

EASY

Physics>Waves and Oscillations>Oscillations>Energy of a Particle Performing S.H.M

At which position, the total energy of a particle executing linear S.H.M. is purely potential?

MEDIUM

Physics>Waves and Oscillations>Oscillations>Energy of a Particle Performing S.H.M

A body is executing S.H.M. At a displacement

x

its potential energy is

9 J

and at a displacement

y

its potential energy is

16 J

. The potential energy at displacement

(x + y)

MEDIUM

Physics>Waves and Oscillations>Oscillations>Energy of a Particle Performing S.H.M

A particle executes simple harmonic motion with time period

T

, amplitude

A

and maximum speed

V_{m}

. The particle is at the mean position when

t = 0

. If

y

is the displacement from the mean position and

v

is the speed, then choose the correct statement(s) from the following in the time interval

0 \leq t \leq T / 4

MEDIUM

Physics>Waves and Oscillations>Oscillations>Energy of a Particle Performing S.H.M

A particle starts executing simple harmonic motion

(SHM)

of amplitude

a

and total energy

E .

At any instant, its kinetic energy is

\frac{3 E}{4}

, then its displacement

y

is given by:

EASY

Physics>Waves and Oscillations>Oscillations>Energy of a Particle Performing S.H.M

Total energy of a particle performing S.H.M. is NOT proportional to

MEDIUM

Physics>Waves and Oscillations>Oscillations>Energy of a Particle Performing S.H.M

The total energy of a body executing simple harmonic motion is

E

. The kinetic energy when the displacement is

1 / 3

of the amplitude

What is the total energy in simple harmonic motion at the mean position ?

Important Questions on Oscillations

Learn and Prepare for any exam you want !