Two dice are thrown independently. Let A be the event that the number appeared on the 1 st die is less than the number appeared on the 2 nd die, B be the event that the number appeared on the 1 st die is even and that on the second die is odd, and C be the event that the number appeared on the 1 st die is odd and that on the 2 nd is even. Then

The number of favourable cases of the event ( A ∪ B ) ∩ C is 6

The number of favourable cases of the events A , B and C are 15 , 6 and 6 respectively

MEDIUM

JEE Main

IMPORTANT

Earn 100

When a certain biased die is rolled, a particular face occurs with probability $\frac{1}{6} - x$ and its opposite face occurs with probability $\frac{1}{6} + x .$ All other faces occur with probability $\frac{1}{6} .$

Note that opposite faces sum to $7$ in any die. If $0 < x < \frac{1}{6},$ and the probability of obtaining total sum $= 7,$ when such a die is rolled twice, is $\frac{13}{96},$ then the value of $x$ is

50% studentsanswered this correctly

Important Questions on Probability

MEDIUM

JEE Main

IMPORTANT

EMBIBE CHAPTER WISE PREVIOUS YEAR PAPERS FOR MATHEMATICS>Chapter 9 - Probability>JEE Main - 27 August 2021 Shift 2>Q 4

Each of the persons

A

and

B

independently tosses three fair coins. The probability that both of them get the same number of heads is:

EASY

JEE Main

IMPORTANT

EMBIBE CHAPTER WISE PREVIOUS YEAR PAPERS FOR MATHEMATICS>Chapter 9 - Probability>JEE Main - 31 August 2021 Shift 1>Q 5

An electric instrument consists of two units. Each unit must function independently for the instrument to operate. The probability that the first unit functions is

0.9

and that of the second unit is

0.8 .

The instrument is switched on and it fails to operate. If the probability that only the first unit failed and second unit is functioning is

p,

then

98 p

is equal to

MEDIUM

JEE Main

IMPORTANT

EMBIBE CHAPTER WISE PREVIOUS YEAR PAPERS FOR MATHEMATICS>Chapter 9 - Probability>JEE Main - 31 August 2021 Shift 2>Q 6

Let

S = {1, 2, 3, 4, 5, 6} .

Then the probability that a randomly chosen onto function

g

from

S

S

satisfies

g (3) = 2 g (1)

is :

HARD

JEE Main

IMPORTANT

EMBIBE CHAPTER WISE PREVIOUS YEAR PAPERS FOR MATHEMATICS>Chapter 9 - Probability>JEE Main - 1 September 2021 Shift 2>Q 7

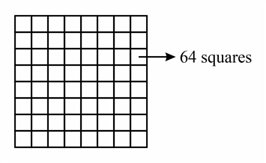
Two squares are chosen at random on a chessboard (see figure). The probability that they have a side in common is :

Question Image

MEDIUM

JEE Main

IMPORTANT

EMBIBE CHAPTER WISE PREVIOUS YEAR PAPERS FOR MATHEMATICS>Chapter 9 - Probability>JEE Main - 1 September 2021 Shift 2>Q 8

Let $X$ be a random variable with distribution.

$x$	$- 2$	$- 1$	$3$	$4$	$6$
$P (X = x)$	$\frac{1}{5}$	$a$	$\frac{1}{3}$	$\frac{1}{5}$	$b$

If the mean of $X$ is $2.3$ and variance of $X$ is $σ^{2},$ then $100 σ^{2}$ is equal to :

HARD

JEE Main

IMPORTANT

EMBIBE CHAPTER WISE PREVIOUS YEAR PAPERS FOR MATHEMATICS>Chapter 9 - Probability>JEE Main - 20 July 2021 Shift 1>Q 9

Words with or without meaning are to be formed using all the letters of the word

EXAMINATION

. The probability that the letter

M

appears at the fourth position in any such word is:

HARD

JEE Main

IMPORTANT

EMBIBE CHAPTER WISE PREVIOUS YEAR PAPERS FOR MATHEMATICS>Chapter 9 - Probability>JEE Main - 20 July 2021 Shift 1>Q 10

The probability of selecting integers

a \in [- 5, 30]

such that

x^{2} + 2 (a + 4) x - 5 a + 64 > 0

, for all

x \in R

, is:

HARD

JEE Main

IMPORTANT

EMBIBE CHAPTER WISE PREVIOUS YEAR PAPERS FOR MATHEMATICS>Chapter 9 - Probability>JEE Main - 20 July 2021 Shift 2>Q 11

Let

A, B

and

C

be three events such that the probability that exactly one of

A

and

B

occurs is

(1 - k),

the probability that exactly one of

B

and

C

occurs is

(1 - 2 k),

the probability that exactly one of

C

and

A

occurs is

(1 - k)

and the probability of all

A, B

and

C

occur simultaneously is

k^{2},

where

0 < k < 1 .

Then the probability that at least one of

A, B

and

C

occur is:

Important Questions on Probability

Learn and Prepare for any exam you want !