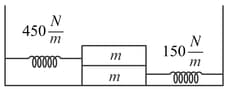
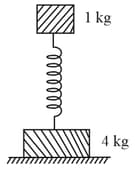
When the system shown in the diagram is in equilibrium the right spring is stretched by 1cm The coefficient of static friction between the blocks is 03 There is no friction between the bottom block and the supporting surface The force constants of the springs are 150Nm1 and 450Nm1 The blocks have equal mass of 2kg each Find the maximum amplitude in cm of the oscillations of the system shown in the figure that does not allow the top block to slide on the bottom

MEDIUM

Physical Sciences>Energy>Plan and conduct an investigation to provide evidence that the transfer of thermal energy when two components of different temperature are combined within a closed system results in a more uniform energy distribution among the components in the system (second law of thermodynamics).>Conservation of Energy and Energy Transfer - Energy cannot be created or destroyed, but it can be transported from one place to another and transferred between systems.Uncontrolled systems always evolve toward more stable states—that is, toward more uniform energy distribution (e.g., water flows downhill, objects hotter than their surrounding environment cool down)

A mass

M

is suspended from a light spring. An additional mass $m$ added displaces the spring further by a distance

X .

Now the combined mass will oscillate on the spring with period

HARD

Physical Sciences>Energy>Plan and conduct an investigation to provide evidence that the transfer of thermal energy when two components of different temperature are combined within a closed system results in a more uniform energy distribution among the components in the system (second law of thermodynamics).>Conservation of Energy and Energy Transfer - Energy cannot be created or destroyed, but it can be transported from one place to another and transferred between systems.Uncontrolled systems always evolve toward more stable states—that is, toward more uniform energy distribution (e.g., water flows downhill, objects hotter than their surrounding environment cool down)

Two blocks of masses

m_{1} = 1 kg

and

m_{2} = 2 kg

are connected by a spring of spring constant

24 N m^{- 1}

and is placed on a horizontal frictionless surface. The block

m_{1}

is imparted an initial velocity

12 cm s^{- 1}

which produces maximum compression in the spring towards

m_{2}

. The amplitude of oscillation is

EASY

Physical Sciences>Energy>Plan and conduct an investigation to provide evidence that the transfer of thermal energy when two components of different temperature are combined within a closed system results in a more uniform energy distribution among the components in the system (second law of thermodynamics).>Conservation of Energy and Energy Transfer - Energy cannot be created or destroyed, but it can be transported from one place to another and transferred between systems.Uncontrolled systems always evolve toward more stable states—that is, toward more uniform energy distribution (e.g., water flows downhill, objects hotter than their surrounding environment cool down)

A

10 Kg

collar is attached to a spring (spring constant

600 N / m

). It slides without friction over a horizontal rod. The collar is displaced from its equilibrium position by

20 cm

and released. What is the speed of the oscillation?

EASY

Physical Sciences>Energy>Plan and conduct an investigation to provide evidence that the transfer of thermal energy when two components of different temperature are combined within a closed system results in a more uniform energy distribution among the components in the system (second law of thermodynamics).>Conservation of Energy and Energy Transfer - Energy cannot be created or destroyed, but it can be transported from one place to another and transferred between systems.Uncontrolled systems always evolve toward more stable states—that is, toward more uniform energy distribution (e.g., water flows downhill, objects hotter than their surrounding environment cool down)

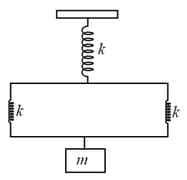
Two identical springs of spring constant $2 k$ are attached to a block of mass $m$ and to fixed support (see figure). When the mass is displaced from equilibrium position on either side, it executes simple harmonic motion. The time period of oscillations of this system is :

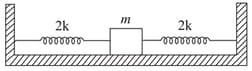
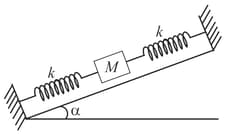
Question Image

EASY

Physical Sciences>Energy>Plan and conduct an investigation to provide evidence that the transfer of thermal energy when two components of different temperature are combined within a closed system results in a more uniform energy distribution among the components in the system (second law of thermodynamics).>Conservation of Energy and Energy Transfer - Energy cannot be created or destroyed, but it can be transported from one place to another and transferred between systems.Uncontrolled systems always evolve toward more stable states—that is, toward more uniform energy distribution (e.g., water flows downhill, objects hotter than their surrounding environment cool down)

A spring whose unstrentches length is

l

has a force constant

k .

The spring is cut into two pieces of unstretches lengths

l_{1}

and

l_{2}

where,

l_{1} = n l_{2}

and

n

is an integer. The ratio

k_{1} / k_{2}

of the corresponding force constants,

k_{1}

and

k_{2}

will be:

EASY

Physical Sciences>Energy>Plan and conduct an investigation to provide evidence that the transfer of thermal energy when two components of different temperature are combined within a closed system results in a more uniform energy distribution among the components in the system (second law of thermodynamics).>Conservation of Energy and Energy Transfer - Energy cannot be created or destroyed, but it can be transported from one place to another and transferred between systems.Uncontrolled systems always evolve toward more stable states—that is, toward more uniform energy distribution (e.g., water flows downhill, objects hotter than their surrounding environment cool down)

In the given figure, a body of mass $M$ is held between two massless springs, on a smooth inclined plane. The free ends of the springs are attached to firm supports. If each spring has spring constant $k,$ the frequency of oscillation of given body is:

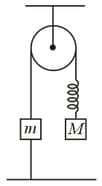
Question Image

HARD

Physical Sciences>Energy>Plan and conduct an investigation to provide evidence that the transfer of thermal energy when two components of different temperature are combined within a closed system results in a more uniform energy distribution among the components in the system (second law of thermodynamics).>Conservation of Energy and Energy Transfer - Energy cannot be created or destroyed, but it can be transported from one place to another and transferred between systems.Uncontrolled systems always evolve toward more stable states—that is, toward more uniform energy distribution (e.g., water flows downhill, objects hotter than their surrounding environment cool down)

An arrangement of spring, strings, pulley and masses is shown in the figure below.
Question Image

The pulley and the strings are massless and

M > m

. The spring is light with spring constant

k

. If the string connecting

m

to the ground is detached, then immediately after detachment

MEDIUM

Physical Sciences>Energy>Plan and conduct an investigation to provide evidence that the transfer of thermal energy when two components of different temperature are combined within a closed system results in a more uniform energy distribution among the components in the system (second law of thermodynamics).>Conservation of Energy and Energy Transfer - Energy cannot be created or destroyed, but it can be transported from one place to another and transferred between systems.Uncontrolled systems always evolve toward more stable states—that is, toward more uniform energy distribution (e.g., water flows downhill, objects hotter than their surrounding environment cool down)

A spring is stretched by

5 cm

by a force

10 N

. The time period of the oscillations when a mass of

2 kg

is suspended by it is :

EASY

Physical Sciences>Energy>Plan and conduct an investigation to provide evidence that the transfer of thermal energy when two components of different temperature are combined within a closed system results in a more uniform energy distribution among the components in the system (second law of thermodynamics).>Conservation of Energy and Energy Transfer - Energy cannot be created or destroyed, but it can be transported from one place to another and transferred between systems.Uncontrolled systems always evolve toward more stable states—that is, toward more uniform energy distribution (e.g., water flows downhill, objects hotter than their surrounding environment cool down)

If the mass shown in figure is slightly displaced and then let go, then the system shall oscillate with a time period of
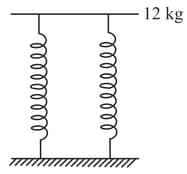
Question Image

EASY

Physical Sciences>Energy>Plan and conduct an investigation to provide evidence that the transfer of thermal energy when two components of different temperature are combined within a closed system results in a more uniform energy distribution among the components in the system (second law of thermodynamics).>Conservation of Energy and Energy Transfer - Energy cannot be created or destroyed, but it can be transported from one place to another and transferred between systems.Uncontrolled systems always evolve toward more stable states—that is, toward more uniform energy distribution (e.g., water flows downhill, objects hotter than their surrounding environment cool down)

A tray of mass $12 kg$ is supported by two identical springs as shown in figure. When the tray is pressed down slightly and then released, it executes SHM with a time period of $1.5 s$ . The spring constant of each spring is

Question Image

MEDIUM

Physical Sciences>Energy>Plan and conduct an investigation to provide evidence that the transfer of thermal energy when two components of different temperature are combined within a closed system results in a more uniform energy distribution among the components in the system (second law of thermodynamics).>Conservation of Energy and Energy Transfer - Energy cannot be created or destroyed, but it can be transported from one place to another and transferred between systems.Uncontrolled systems always evolve toward more stable states—that is, toward more uniform energy distribution (e.g., water flows downhill, objects hotter than their surrounding environment cool down)

If two similar springs each of spring constant

K_{1}

are joined in series, the new spring constant and time period would be changed by a factor:

HARD

Physical Sciences>Energy>Plan and conduct an investigation to provide evidence that the transfer of thermal energy when two components of different temperature are combined within a closed system results in a more uniform energy distribution among the components in the system (second law of thermodynamics).>Conservation of Energy and Energy Transfer - Energy cannot be created or destroyed, but it can be transported from one place to another and transferred between systems.Uncontrolled systems always evolve toward more stable states—that is, toward more uniform energy distribution (e.g., water flows downhill, objects hotter than their surrounding environment cool down)

Two bodies of masses

1 kg

and

4 kg

are connected to a vertical spring, as shown in the figure. The smaller mass executes simple harmonic motion of angular frequency

25 rad s^{- 1}

, and amplitude

1.6 cm

while the bigger mass remains stationary on the ground. The maximum force exerted by the system on the floor is (take

g = 10 m s^{- 2}

).

EASY

Physical Sciences>Energy>Plan and conduct an investigation to provide evidence that the transfer of thermal energy when two components of different temperature are combined within a closed system results in a more uniform energy distribution among the components in the system (second law of thermodynamics).>Conservation of Energy and Energy Transfer - Energy cannot be created or destroyed, but it can be transported from one place to another and transferred between systems.Uncontrolled systems always evolve toward more stable states—that is, toward more uniform energy distribution (e.g., water flows downhill, objects hotter than their surrounding environment cool down)

Two particles

A

and

B

of equal masses are suspended from two massless springs of spring constants

K_{1}

and

K_{2}

respectively.If the maximum velocities during oscillations are equal, the ratio of the amplitude of

A

and

B

is

MEDIUM

Physical Sciences>Energy>Plan and conduct an investigation to provide evidence that the transfer of thermal energy when two components of different temperature are combined within a closed system results in a more uniform energy distribution among the components in the system (second law of thermodynamics).>Conservation of Energy and Energy Transfer - Energy cannot be created or destroyed, but it can be transported from one place to another and transferred between systems.Uncontrolled systems always evolve toward more stable states—that is, toward more uniform energy distribution (e.g., water flows downhill, objects hotter than their surrounding environment cool down)

In the given figure, a mass $M$ is attached to a horizontal spring which is fixed on one side to a rigid support. The spring constant of the spring is $k .$ The mass oscillates on a frictionless surface with time period $T$ and amplitude $A .$ When the mass is in equilibrium position, as shown in the figure, another mass $m$ is gently fixed upon it. The new amplitude of oscillation will be:

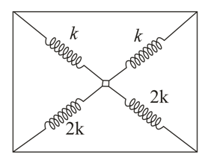
Question Image

EASY

Physical Sciences>Energy>Plan and conduct an investigation to provide evidence that the transfer of thermal energy when two components of different temperature are combined within a closed system results in a more uniform energy distribution among the components in the system (second law of thermodynamics).>Conservation of Energy and Energy Transfer - Energy cannot be created or destroyed, but it can be transported from one place to another and transferred between systems.Uncontrolled systems always evolve toward more stable states—that is, toward more uniform energy distribution (e.g., water flows downhill, objects hotter than their surrounding environment cool down)

A mass

2 kg

is suspended from two coupled springs connected in series. The force constants for springs are

24.5 N m^{- 1}

and

25.5 N m^{- 1}

. The time period of the suspended mass is

MEDIUM

Physical Sciences>Energy>Plan and conduct an investigation to provide evidence that the transfer of thermal energy when two components of different temperature are combined within a closed system results in a more uniform energy distribution among the components in the system (second law of thermodynamics).>Conservation of Energy and Energy Transfer - Energy cannot be created or destroyed, but it can be transported from one place to another and transferred between systems.Uncontrolled systems always evolve toward more stable states—that is, toward more uniform energy distribution (e.g., water flows downhill, objects hotter than their surrounding environment cool down)

A heavy brass sphere is hung from a spring and it executes vertical vibrations with period

T .

The sphere is now immersed in a non-viscous liquid with a density

(1 / 10)^{th}

that of brass. When set into vertical vibrations with the sphere remaining inside liquid all the time, the time period will be

MEDIUM

Physical Sciences>Energy>Plan and conduct an investigation to provide evidence that the transfer of thermal energy when two components of different temperature are combined within a closed system results in a more uniform energy distribution among the components in the system (second law of thermodynamics).>Conservation of Energy and Energy Transfer - Energy cannot be created or destroyed, but it can be transported from one place to another and transferred between systems.Uncontrolled systems always evolve toward more stable states—that is, toward more uniform energy distribution (e.g., water flows downhill, objects hotter than their surrounding environment cool down)

A spring is stretched by

0.40 m

when a mass of

0.6 kg

is suspended from it. The period of oscillations of the spring loaded by

255 gm

and put to oscillations is close to

{}_{-}{(g = 10 m s^{- 2})}

HARD

Physical Sciences>Energy>Plan and conduct an investigation to provide evidence that the transfer of thermal energy when two components of different temperature are combined within a closed system results in a more uniform energy distribution among the components in the system (second law of thermodynamics).>Conservation of Energy and Energy Transfer - Energy cannot be created or destroyed, but it can be transported from one place to another and transferred between systems.Uncontrolled systems always evolve toward more stable states—that is, toward more uniform energy distribution (e.g., water flows downhill, objects hotter than their surrounding environment cool down)

A particle of mass $m$ is attached to four springs with spring constant $k, k, 2 k$ and $2 k$ as shown in the figure. Four springs are attached to the four corners of a square and a particle is placed at the center. If the particle is pushed slightly towards any side of the square and released, the period of oscillation will be

Question Image

MEDIUM

Physical Sciences>Energy>Plan and conduct an investigation to provide evidence that the transfer of thermal energy when two components of different temperature are combined within a closed system results in a more uniform energy distribution among the components in the system (second law of thermodynamics).>Conservation of Energy and Energy Transfer - Energy cannot be created or destroyed, but it can be transported from one place to another and transferred between systems.Uncontrolled systems always evolve toward more stable states—that is, toward more uniform energy distribution (e.g., water flows downhill, objects hotter than their surrounding environment cool down)

A silver atom in a solid oscillates in simple harmonic motion in some direction with a frequency of

10^{12} s^{- 1}

. What is the force constant of the bonds connecting one atom with the other? (Mole wt. of silver,

= 108 g {mol}^{- 1}

and Avogadro number

= 6.02 \times 10^{23}

)

EASY

Physical Sciences>Energy>Plan and conduct an investigation to provide evidence that the transfer of thermal energy when two components of different temperature are combined within a closed system results in a more uniform energy distribution among the components in the system (second law of thermodynamics).>Conservation of Energy and Energy Transfer - Energy cannot be created or destroyed, but it can be transported from one place to another and transferred between systems.Uncontrolled systems always evolve toward more stable states—that is, toward more uniform energy distribution (e.g., water flows downhill, objects hotter than their surrounding environment cool down)

A body of mass,

m

is attached to the lower end of a spring whose upper end is fixed. The spring has negligible mass. When the mass

m

is slightly pulled down and released, it oscillates with a time period of

3 s

. When the mass

m

is increased by

1 kg

, the time period of oscillations becomes

5 s

. The value of

m

in

kg

is

Learn and Prepare for any exam you want !