When they are switched on, certain small devices independently produce outputs of $1, 2$ or $3$ volts with respective probabilities of $0.3, 0.6$ and $0.1$. Find the probability that three of these devices produce an output with a sum of $5$ or $6$ volts.

One hundred people are attending a conference. The following Venn diagram shows how many are male $\left(M\right)$, have brown eyes $\left(BE\right)$ and are right-handed $\left(RH\right)$.

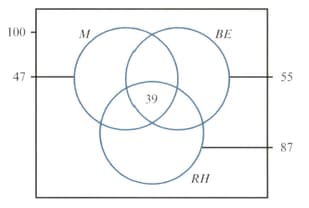
Given that there are $43$ males with brown eyes, $42$ right-handed males and 46 right-handed people with brown eyes, copy and complete the Venn diagram.

One hundred people are attending a conference. The following Venn diagram shows how many are male $\left(M\right)$, have brown eyes $\left(BE\right)$ and are right-handed $\left(RH\right)$.

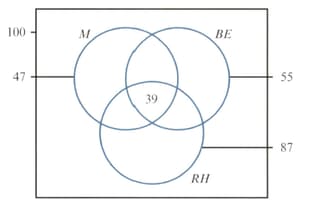
Two attendees are selected at random. Find the probability that they are both females who are not right-handed.       [correct up to five decimal places]

One hundred people are attending a conference. The following Venn diagram shows how many are male $\left(M\right)$, have brown eyes $\left(BE\right)$ and are right-handed $\left(RH\right)$.

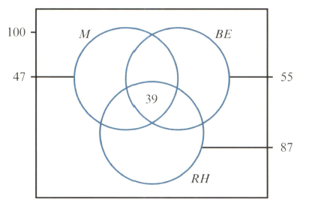
Two attendees are selected at random. Find the probability that exactly one of them is right-handed, given that neither of them have brown eyes.      [correct up to three decimal places]

A student travels to college by either of two routes, $A$ or $B$. The probability that they use route $A$ is $0.3$, and the probability that they are passed by a bus on their way to college on any particular day is $0.034$. They are twice as likely to be passed by a bus when they use route $B$ as when they use route $A$.

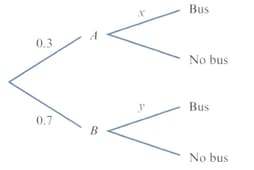
Use the tree diagram opposite to form and solve a pair of simultaneous equations in $x$ and $y$.

A student travels to college by either of two routes, $A$ or $B$. The probability that they use route $A$ is $0.3$, and the probability that they are passed by a bus on their way to college on any particular day is $0.034$. They are twice as likely to be passed by a bus when they use route $B$ as when they use route $A$.

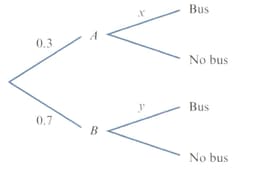
Find the probability that the student uses route $B$, given that they are not passed by a bus on their way to college.   [correct up to three decimal places]

Two ordinary fair dice are rolled. If the first shows a number less than $3$ , then the score is the mean of the numbers obtained; otherwise the score is equal to half the absolute (non-negative) difference between the numbers obtained. Find the probability that the score is:

positive

Two ordinary fair dice are rolled. If the first shows a number less than $3$ , then the score is the mean of the numbers obtained; otherwise the score is equal to half the absolute (non-negative) difference between the numbers obtained. Find the probability that the score is:

greater than $1$ , given that it is less than $2$

Two ordinary fair dice are rolled. If the first shows a number less than $3$ , then the score is the mean of the numbers obtained; otherwise the score is equal to half the absolute (non-negative) difference between the numbers obtained. Find the probability that the score is:

less than $2$, given that it is greater than $1$