Where does the orthocentre lie in the case of a right angled triangle?
Important Questions on Geometry
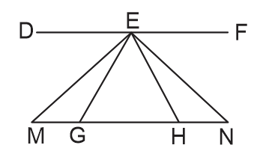
In the above figure, is parallel to . is an isosceles triangle, where and . If and are the bisectors of the and , then
Show that .
In an obtuse - angled triangle, the obtuse angled is . Find the angle made on its orthocentre.
The point of two external angle bisector for any side of a triangle and internal angle bisector of the angle opposite side chosen is called
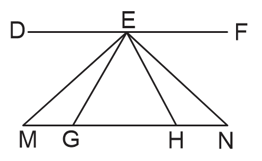
In the above figure, is parallel to . is an isosceles triangle, where and . If and are the bisectors of the and , then
Show that .
If the coordinates of the mid-points of the sides of a triangle are and . Find its centroid.
Where does the orthocentre lie in the case of an obtuse-angled triangle?
In the median and passes through the point . If then, find .
Where does the orthocentre lie in the case of an acute-angled triangle?
In figure, point is the point of concurrence of the medians of . If , find the lengths of .
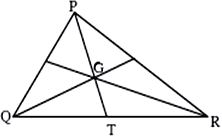
is at the origin, then
Find in how many points do the three medians of a triangle meet.
In the median and passes through the point . If then find (in ) (correct up to one decimal place)
The point of intersection of the perpendicular bisectors of the sides of a triangle is called:

