Which of the following gases has maximum rms speed at a given temperature?

1. Kinetic Theory of Gases:
The kinetic theory of gases is a simple, significant model of the thermodynamic behavior of gases. The model describes a gas as a large number of identical submicroscopic particles (atoms or molecules), all of which are in constant, rapid, and random motion.
2. Some Assumptions of Ideal Gas:
It attempts to develop a model of the molecular behavior which should result in the observed behavior of an ideal gas. It is based on the following assumptions:
(i) The gas consists of very small particles (molecules). All molecules of a given gas are identical.
(ii) The rapidly moving molecules constantly collide among themselves and with the walls of the container. All these collisions are perfectly elastic, which means the molecules are perfect rigid spheres.
(iii) The size of the molecule is negligible in comparison to the distance between the molecules.
(iv) The sum of volumes of molecules is negligible in comparison to the volume of gas.
(v) Molecules of gas keep on moving randomly in all possible directions with all possible velocities.
(vi) The speed of gas molecules lies between zero and infinity.
(vii) The number of particles is so large that statistical treatment can be applied.
(viii) The time spent in a collision between two molecules is negligible in comparison to the time between two successive collisions.
(ix) The number of collisions per unit volume in a gas remains constant.
(x) For an ideal gas, intermolecular forces are negligible (except during collision).
(xi) Gravitational attraction among the molecules is ineffective due to extremely small masses and very high speeds of molecules.
(xii) Molecules constantly collide with the walls of the container due to which their momentum changes. The change in momentum is transferred to the walls of the container. Consequently, the pressure is exerted by gas molecules on the walls of the container.
(xiii) The density of the gas is constant at all points of the container.
3. Gas Laws:
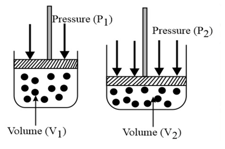
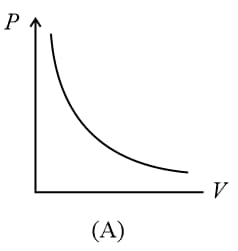
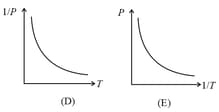
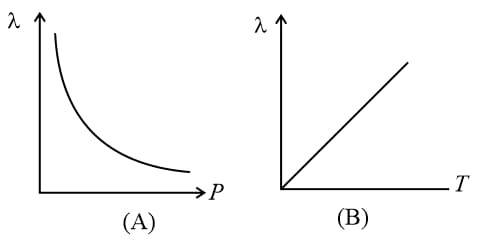
(i) Boyle’s law: At constant temperature, the volume of a gas is inversely proportional to its pressure for a given mass of an ideal gas, i.e.,
$P\propto \frac{1}{V}$ or $PV=$ constant,

$\Rightarrow P_1{V}_1=P_2{V}_2$

(ii) For a given mass, at a constant temperature, $\frac{P}{\rho }=$ constant or $\frac{P_1}{{\rho }_1}=\frac{P_2}{{\rho }_2}$, where $P$ is pressure and $\rho$ is density.
(iii) $PV=P\left(\frac{N}{n}\right)=$ constant $\Rightarrow \frac{P}{n}=$ constant or $\frac{P_1}{n_1}=\frac{P_2}{n_2}$, where $n$ is the number of molecules per unit volume.
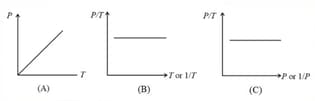
(iv) Graphs: If the mass of the gas $m$ and temperature $T$ are constants, then

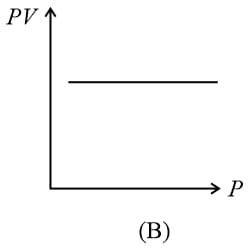
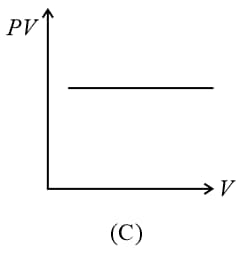
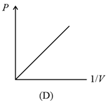
4. Charle's Law:
The volume of the given mass of a gas is directly proportional to its absolute temperature at constant pressure, i.e.,

$V\propto T\Rightarrow \frac{V}{T}=\mathrm{constant} \Rightarrow \frac{V_1}{T_1}=\frac{V_2}{T_2}$
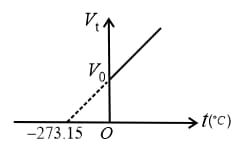
(i) $\frac{V}{T}=\frac{m}{\rho T}=$ constant (As volume $V=\frac{m}{\rho }$) or $\rho T=$ constant $\Rightarrow {\rho }_1{T}_1={\rho }_2{T}_2$

(ii) Graphs: If $m$ and $P$ are constants,

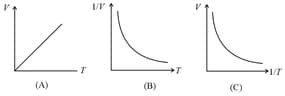
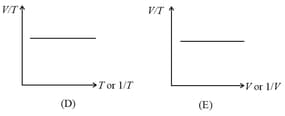
5. Gay-Lussac’s Law or Pressure Law:

The pressure of a given mass of a gas is directly proportional to its absolute temperature at constant volume.

P∝T or $\frac{P}{T}=$ constant $\Rightarrow \frac{P_1}{T_1}=\frac{P_2}{T_2}$

(i) Pressure at temperature t is, $P_{\mathrm{t}}=P_0\left[1+\frac{1}{273.15}t\right]$

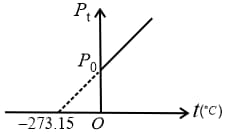
(ii) Graphs: If $m$ and $V$ are constants, then

6. Avogadro’s Law:
Equal volume of all the gases under similar conditions of temperature and pressure contain equal number of molecules, i.e., N1=N2.
7. Dalton’s Law of Partial Pressures:
The total pressure exerted by a mixture of non-reacting gases occupying a vessel is equal to the sum of the individual pressures which each gas exerts if it alone occupies the same volume at a given temperature.
For $n$ gases $P=P_1+P_2+P_3+\cdots P_n$, where $P=$ pressure exerted by mixture and $P_1,P_2,P_3,\dots P_n=$ partial pressures of component gases.

8. Equation of State or Ideal Gas Equation:
The equation which relates the pressure $\left(P\right)$, volume $\left(V\right)$ and temperature $\left(T\right)$ of the given state of an ideal gas is known as the ideal gas equation or equation of state.
(i) For $1$ mole of gas, $PV=RT$, where $R=$ universal gas constant.
(ii) For $\mu$ mole of gas, $PV=\mu RT$, where $R=$ universal gas constant.
(iii) For $1$ molecule of gas, PV=RNAT=kT, where $k=$ Boltzmann's constant.
(iv) For $N$ molecule of gas, PV=NkT, where $k=$ Boltzmann's constant.
(v) For $1 \mathrm{g}$ of gas, $PV=\left(\frac{R}{M}\right)T=rT$, where r is specific gas constant.
(vi) For m $\mathrm{g}$ of gas, $PV=\left(\frac{R}{M}\right)T=mrT$, where r is specific gas constant.
9. Universal Gas Constant ($R$):
Universal gas constant signifies the work done by (or) on gas per mole per Kelvin, i.e., $R=\frac{PV}{\mu T}=\frac{\text{Pressure}\times \text{Volume}}{\mu \times \text{Temperature}}=\frac{\text{Work done}}{\mu \mathrm{ }\times \text{Temperature}}$

(i) At S.T.P. the value of the universal gas constant is the same for all gases.
$R=8.31 \mathrm{J} {\mathrm{mole}}^{-1} {\mathrm{K}}^{-1}=2 \mathrm{Cal} {\mathrm{mole}}^{-1} {\mathrm{K}}^{-1}$.
(ii) $\mathrm{S}.\mathrm{I}.$ unit: $\mathrm{J}\mathrm{ }\mathrm{m}\mathrm{o}{\mathrm{l}}^{-1}{\mathrm{K}}^{-1}$.

(iii) Dimensional formula: ${\mathrm{ML}}^2{\mathrm{T}}^{-2}{\mathrm{K}}^{-1}{\mathrm{mol}}^{-1}$.

10. Boltzmann’s Constant ($k$):
(i) It is represented by per mole gas constant, i.e., $k=\frac{R}{N}=\frac{8.31}{6.023\times 10^{23}}=1.38\times 10^{-23}\hspace{0.33em}\mathrm{J}\mathrm{ }{\mathrm{K}}^{-1}$.
(ii) Its dimensional formula: ${\mathrm{ML}}^2{\mathrm{T}}^{-2}{\mathrm{K}}^{-1}$.

11. Specific Gas Constant $\left(\mathbf{r}\right)$:
(i) It is represented by the gas constant per gram, i.e., $r=\frac{R}{M}$.
(ii) S.I. unit is $\mathrm{J} {\mathrm{g}}^{-1} {\mathrm{K}}^{-1}$.
(iii) Dimensional formuka: ${\mathrm{L}}^2{\mathrm{T}}^{-2}{\mathrm{K}}^{-1}$.
(iv) Since the value of $M$ is different for different gases, the value of r is different for different gases, e.g., it is maximum for hydrogen $r_{{\mathrm{H}}_2}=\frac{R}{2}$.
12. Pressure of an Ideal Gas:
Consider an ideal gas (consisting of $N$ molecules each of mass $m$) enclosed in a cubical box of side L.

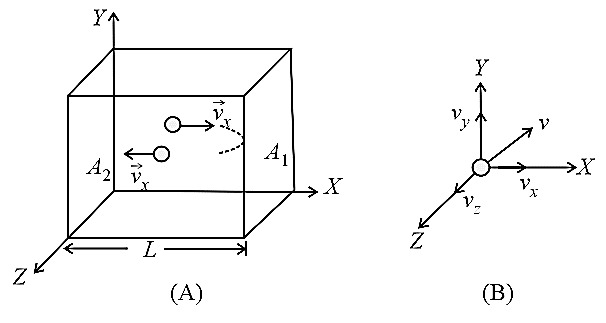
(i) Instantaneous velocity:
Any molecule of gas moves with velocity v→ in any direction, where $\overrightarrow{v}=v_{\mathrm{x}}\hat{\mathrm{i}}+v_{\mathrm{y}}\hat{\mathrm{j}}+v_{\mathrm{z}}\hat{\mathrm{k}} \Rightarrow v=\sqrt{v_{\mathrm{x}}^2+v_{\mathrm{y}}^2+v_{\mathrm{z}}^2}$.
Due to the random motion of molecule, $v_{\mathrm{x}}=v_{\mathrm{y}}=v_{\mathrm{z}}\Rightarrow$$v^2=3v_{\mathrm{x}}^2=3v_{\mathrm{y}}^2=3v_{\mathrm{z}}^2$.

(ii) Time during collision:
The time between two successive collisions with the wall is A1.

$\mathrm{\Delta }t=\frac{\text{Distance travelled by molecule between two successive collisions}}{\text{Velocity of molecule}}=\frac{2L}{v_{\mathrm{x}}}$

(iii) Collision frequency $\left(n\right)$:
It means the number of collisions per second. Hence $n=\frac{1}{\mathrm{\Delta }t}=\frac{v_{\mathrm{x}}}{2L}$.
(iv) Change in the momentum:
This molecule collides with the wall $\left(A_1\right)$ with velocity $v_{\mathrm{x}}$ and rebounds with velocity $-v_{\mathrm{x}}$.

The change in the momentum of the molecule $\mathrm{\Delta }p=\left(-m{v}_{\mathrm{x}}\right)-\left(m{v}_{\mathrm{x}}\right)=-2m{v}_{\mathrm{x}}$.

(v) Force on the wall:
Force exerted by a single molecule on the shaded wall is equal to the rate at which the momentum is transferred to the wall by this molecule, i.e., $F_{\mathrm{Single} \mathrm{molecule}}=\frac{\mathrm{\Delta }p}{\mathrm{\Delta }t}=\frac{2m{v}_{\mathrm{x}}}{\left(2L/v_{\mathrm{x}}\right)}=\frac{m{v}_{\mathrm{x}}^2}{L}$

The total force on the wall A1 due to all the molecules is
, where   mean square of $x$ component of the velocity.

(vi) Pressure:
Now the pressure is defined as force per unit area; hence, the pressure on the shaded wall, 

For any molecule, the mean square velocity, ;

By symmetry

Total pressure inside the container, $P=\frac{1}{3}\frac{mN}{V}{v}_{\mathrm{rms}}^2$

(vii) Relation between pressure and kinetic energy:

(a) As we know $P=\frac{1}{3}\frac{mN}{V}{v}_{\mathrm{rms}}^2=\frac{1}{3}\frac{M}{V}{v}_{\mathrm{rms}}^2\Rightarrow P=\frac{1}{3}\rho v_{\mathrm{rms}}^2 \dots \left(\mathrm{i}\right)$ [As $M=mN=$ total mass of the gas and ρ=MV]
(b) Kinetic energy per unit volume $E=\frac{1}{2}\left(\frac{M}{V}\right)v_{\mathrm{rms}}^2=\frac{1}{2}\rho v_{\mathrm{rms}}^2 \dots \left(\mathrm{ii}\right)$
From $\left(\mathrm{i}\right)$ and $\left(\mathrm{ii}\right)$, we get P=23E, i.e., the pressure exerted by an ideal gas is numerically equal to two-thirds of the mean kinetic energy of translation per unit volume of the gas.

13. Effect of Mass, Volume and Temperature on Pressure:

(i) $P=\frac{1}{3}\frac{mN}{V}{v}_{\mathrm{rms}}^2$ or $P\propto \frac{\left(mN\right)T}{V}$ [As $v_{\mathrm{rms}}^2\propto T$]

(ii) If the volume and temperature of a gas are constant $P\propto mN$, i.e., pressure∝(mass of gas). If the mass of gas is increased, then the number of molecules and the number of collisions per second increases. So, the pressure will increase.
(iii) If the mass and temperature of a gas are constant. $P\propto \left(1/V\right)$, i.e., if volume decreases, the number of collisions per second will increase due to lesser effective distance between the walls resulting in greater pressure.
(iv) If the mass and volume of a gas are constant, $P\propto {\left(v_{\mathrm{rms}}\right)}^2\propto T$, i.e., if temperature increases, the mean square speed of gas molecules will increase and as gas molecules are moving faster, they will collide with the walls more often with greater momentum resulting in greater pressure.
14. Various Speeds of Gas Molecules:
The motion of molecules in a gas is characterized by any of the following three speeds:
(i) Root mean square speed:
It is defined as the square root of mean of squares of the speeds of different molecules, 

(a) From the expression of pressure, $P=\frac{1}{3}\rho v_{\mathrm{rms}}^2 \Rightarrow v_{\mathrm{rms}}=\sqrt{\frac{3P}{\rho }}=\sqrt{\frac{3PV}{\mathrm{Mass} \mathrm{of} \mathrm{gas}}}=\sqrt{\frac{3RT}{M}}=\sqrt{\frac{3kT}{m}}$, where
 $\rho =\frac{\text{Mass of gass}}{V}=\text{Density of the gas}$, $M=\mu \times$ (mass of gas), $pV=\mu RT, R=k{N}_{\mathrm{A}},$ $k=$ Boltzmann’s constant, m=MNA= mass of each molecule.
(b) With the rise in temperature $\mathrm{RMS}$ speed of gas molecules increases as $v_{\mathrm{rms}}\propto \sqrt{T}$.
(c) With the increase in molecular weight, $\mathrm{RMS}$ speed of gas molecules decreases as $v_{\mathrm{rms}}\propto \frac{1}{\sqrt{M}}$, e.g., RMS speed of hydrogen molecules is four times that of oxygen molecules at the same temperature.
(d) $\mathrm{RMS}$ speed of gas molecules is 3γ times that of the speed of sound in the gas, as $v_{\mathrm{rms}}=\sqrt{\frac{3RT}{M}}$ and $v_{\mathrm{s}}=\sqrt{\frac{\gamma RT}{M}}\Rightarrow v_{\mathrm{rms}}=\sqrt{\frac{3}{\gamma }}{v}_{\mathrm{s}}$.

(e) $\mathrm{RMS}$ speed of gas molecules does not depend on the pressure of the gas (if the temperature remains constant), because p∝ρ (Boyle’s law) if pressure is increased $n$ times then the density will also increase by $n$ times but $v_{\mathrm{rms}}$ remains constant.
(f) Moon has no atmosphere because $v_{\mathrm{rms}}$ of gas molecules are more than escape velocity $\left(v_{\mathrm{e}}\right)$. A planet or satellite will have an atmosphere only if $v_{\mathrm{rms}}<v_{\mathrm{e}}$.
(g) At $T=0,$ $v_{\mathrm{rms}}=0$, i.e., the $\mathrm{RMS}$ speed of molecules of a gas is zero at $0 \mathrm{K}$. This temperature is called absolute zero.

(ii) Most probable speed:
Most probable speed, $v_{\mathrm{mp}}=\sqrt{\frac{2P}{\rho }}=\sqrt{\frac{2RT}{M}}=\sqrt{\frac{2kT}{m}}$.

(iii) Average speed:
Average speed, $v_{\mathrm{av}}=\sqrt{\frac{8P}{\pi \rho }}=\sqrt{\frac{8}{\pi }\frac{RT}{M}}=\sqrt{\frac{8}{\pi }\frac{kT}{m}}$.

(iv) Maxwell’s law (distribution of molecular speeds):

(a) The $v_{\mathrm{rms}}$ gives us a general idea of molecular speeds in a gas at a given temperature. This does not mean that the speed of each molecule is $v_{\mathrm{rms}}$. Many of the molecules have speed less than $v_{\mathrm{rms}}$ and many have speeds greater than $v_{\mathrm{rms}}$.
(b) Maxwell derived as equation given the distribution of molecules in different speed as follows, $\mathrm{d}N=4\pi N{\left(\frac{m}{2\pi kT}\right)}^{3/2}{v}^2{e}^{-\frac{m{v}^2}{2kT}}\mathrm{d}v$, where $\mathrm{d}N=$ number of molecules with speeds between $v$ and $v+\mathrm{d}v$.

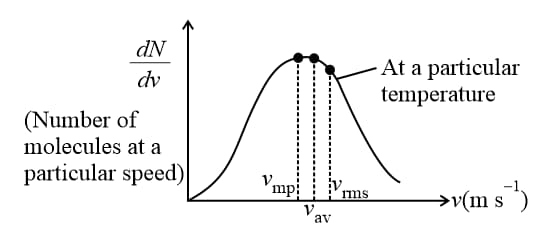
(c) Graph between $\frac{\mathrm{d}N}{\mathrm{d}v}$ (number of molecules at a particular speed) and $v$ (speed of these molecules).
From the graph, it is seen that $\frac{\mathrm{d}N}{\mathrm{d}v}$ is maximum at the most probable speed.
(d) This graph also represents that $v_{\mathrm{rms}}>v_{\mathrm{av}}>v_{\mathrm{mp}}$ $\Rightarrow \sqrt{\frac{3RT}{M}}>\sqrt{\frac{8RT}{\pi M}}>\sqrt{\frac{2RT}{M}}$

(e) Area bounded by this curve with speed axis represents the number of molecules corresponds to that velocity range. This curve is an asymmetric curve.

(v) Effect of temperature on velocity distribution:
With the temperature rise the $\frac{\mathrm{d}N}{\mathrm{d}v}$ versus $v$, the curve shifts towards the right and becomes broader.

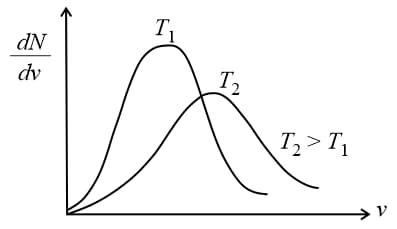
(Because with temperature rise, average molecular speed increases). In the above graph, the area under graph (number of molecules) remains constant for both the graphs.
(vi) Mean free path:

(a) The distance travelled by a gas molecule between two successive collisions is known as a free path.

  $\lambda =\frac{\text{Total distance travelled by a gas molecule between successive collisions}}{\text{Total number of collisions}}$
During two successive collisions, a molecule of gas moves in a straight line with constant velocity.

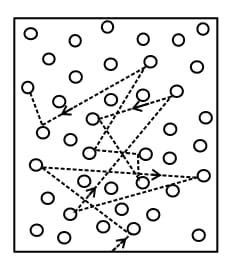
(b) $\lambda =\frac{1}{\sqrt{2}\pi n{d}^2}$, where d= diameter of the molecule, n= number of molecules per unit volume.
(c) As PV=μRT=μRT=μNkT⇒NV=PkT=n= number of molecules per unit volume, so λ=12kTπd2P.
(d) From $\lambda =\frac{1}{\sqrt{2}\pi n{d}^2}=\frac{m}{\sqrt{2}\pi \left(mn\right)d^2}=\frac{m}{\sqrt{2}\pi d^2\rho }$ [As $m=$ mass each molecule, $mn=$ mass per unit volume $=$ density $=\rho$].
(e) If the average speed of molecule is $v$, then λ=v×tN=v×T [As $N=$ number of collisions in time $t$, $T=$ time interval between two collisions].
(f) As λ∝1ρ and λ∝m, i.e., the mean free path is inversely proportional to the density of a gas and directly proportional to the mass of each molecule.

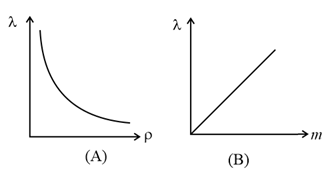
(g) As λ=12kTπd2P

For constant volume and hence constant number density $n$ of gas molecules, PT is constant, so that $\lambda$ will not depend on $P$ and $T$.
But if the volume of a given mass of a gas can change with $P$ or T, then λ∝T at constant pressure and λ∝1P at constant temperature.

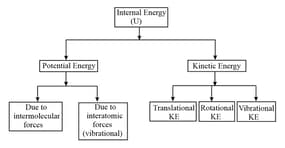
(vii) Degree of freedom:

(a) The term degree of freedom of a system refers to the possible independent motions, systems can have or the total number of independent modes (ways) in which a system can possess energy is called the degree of freedom $\left(f\right)$.
(b) The independent motions can be translational, rotational or vibrational or any combination of these.
(c) General expression for the degree of freedom, f=3A-B; where $A=$ number of independent particles and B= number of independent restrictions.
(d) Monoatomic gas:
Any atom or monoatomic gas molecule has three degrees of freedom associated with translational motion (kinetic energy) of the centre of mass with respect to the $x, y,$ and $z$ axes. So, the degree of freedom is $3$.

(e) Diatomic gas:
Diatomic gas can have only two rotational motions in addition to $3$ translational motions. So, $f=5$.

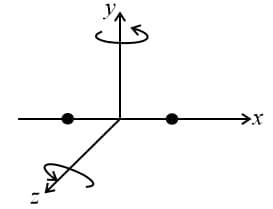
(f) Triatomic gas (non-linear):
A non-linear molecule can rotate about any of three co-ordinate axes. Hence, it has $6$ degrees of freedom: $3$ translational and $3$ rotational.

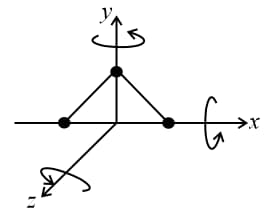
(g) The above degrees of freedom are shown at room temperature. Further at high temperatures, in the case of diatomic or polyatomic molecules, the atoms within the molecule may also vibrate with respect to each other. In such cases, the molecule will have an additional degree of freedom due to vibrational motion.
(h) An object which vibrates in one dimension has two additional degrees of freedom. One for the potential energy and one for the kinetic energy of vibration.
(i) A diatomic molecule that is free to vibrate (in addition to translation and rotation) will have $7\left(2+3+2\right)$ degrees of freedom.

(viii) Kinetic energy of ideal gas:
In ideal gases, the molecules are considered as point particles. The point particles can have only translational motion and thus, only translational energy. For an ideal gas, the internal energy can only be translational kinetic energy. Hence kinetic energy (or internal energy) of $1$ mole ideal gas, $E=\frac{1}{2}M{v}_{\mathrm{rms}}^2=\frac{1}{2}M\times \frac{3RT}{M}=\frac{3}{2}RT$.

(a) Kinetic energy per molecule of gas does not depend upon the mass of the molecule, but only depends upon the temperature of the gas. As E=32kT or E∝T, i.e., molecules of different gases, say $\mathrm{He},\mathrm{ }{\mathrm{H}}_2$ and ${\mathrm{O}}_2$, etc., at the same temperature will have the same translational kinetic energy through their $\mathrm{RMS}$speed is different.
(b) For two gases at the same temperature $m_1(v_{\mathrm{rms}}{)}_1^2=m_2(v_{\mathrm{rms}}{)}_2^2$.
(c) Kinetic energy per mole of gas depends only upon the temperature of the gas.
(d) Kinetic energy per gram of gas depends upon the temperature as well as molecular weight (or mass of one molecule) of the gas,
$E_{\mathrm{gram}}=\frac{3}{2}\frac{k}{m}T$     ⇒ $E_{\mathrm{gram}}\propto \frac{T}{m}$

(e) From the above expressions, the higher is the temperature of the gas, the more will be the average kinetic energy possessed by the gas molecules at $T=0$, $E=0$, i.e., at absolute zero, the molecular motion stops.

(ix) Law of equipartition of energy:
According to this law, for any system in thermal equilibrium, the total energy is equally distributed among its various degree of freedom, and each degree of freedom is associated with an energy 12kT (where k=1.38×10-23 J K-1, $T=$ absolute temperature).

(a) At a given temperature $T$, all ideal gas molecules, no matter what their mass will be, have the same average translational kinetic energy, namely $\frac{3}{2}kT$.
(b) At the same temperature, gases with different degrees of freedom (e.g., He and ${\mathrm{H}}_2$) will have different average energy or internal energy, namely $\frac{f}{2}kT$ ($f$ is different for different gases).

(x) Different energies of a system of the degree of freedom $f$ are as follows,

(a) Total energy associated with each molecule $=\frac{f}{2}kT$
(b) Total energy associated with $N$ molecules $=\frac{f}{2}NkT$
(c) Total energy associated with $1$ mole $=\frac{f}{2}RT$
(d) Total energy associated with $\mu$ mole $=\frac{f}{2}\mu RT$
(e) Total energy associated per gram $=\frac{f}{2}rT$
(f) Total energy associated with $m$ gram $=\frac{f}{2}mrT$

(xi) Specific heat ($C_{\mathrm{P}}$ and $C_{\mathrm{V}}$) of a gas:
The specific heat of gas can have many values, but the following two values are very important.
(a) Molar specific heat at constant volume $\left(C_{\mathrm{V}}\right)$:

 $C_{\mathrm{V}}=M{c}_{\mathrm{V}}=\frac{M{\left(\mathrm{\Delta }Q\right)}_{\mathrm{V}}}{m\mathrm{\Delta }T}=\frac{1}{\mu }\frac{{\left(\mathrm{\Delta }Q\right)}_{\mathrm{V}}}{\mathrm{\Delta }T}$ $\left[\mathrm{As} \mu =\frac{m}{M}\right]$
(b) Molar specific heat at constant from $\left(C_{\mathrm{P}}\right)$:
  $C_{\mathrm{P}}=M{c}_{\mathrm{P}}=\frac{M{\left(\mathrm{\Delta }Q\right)}_{\mathrm{P}}}{m\mathrm{\Delta }T}=\frac{1}{\mu }\frac{{\left(\mathrm{\Delta }Q\right)}_{\mathrm{P}}}{\mathrm{\Delta }T}$ $\left[\mathrm{As} \mu =\frac{m}{M}\right]$
(xii) Mayer's Formula:

(a) It gives the relation between molar specific heats of an ideal gas, $C_{\mathrm{P}}-C_{\mathrm{V}}=R$
(b) Relation between specific heats of gas is $c_{\mathrm{P}}-c_{\mathrm{V}}=\frac{R}{M}$

(xiii) Internal energy of a gas:
The internal energy of a gas is the sum of potential energy and kinetic energy of molecules of the gas. For an ideal gas, intermolecular forces are negligible. So, the potential energy of an ideal gas is taken as zero. The internal energy of the gas is equal to the kinetic energy. 

(a) For a gas at temperature T, Change in energy $\mathrm{\Delta }U=\frac{f}{2}\mu R\mathrm{\Delta }T$
(b) Heat supplied at constant volume, ${\left(\mathrm{\Delta }Q\right)}_{\mathrm{V}}=\mu C_{\mathrm{V}}\mathrm{\Delta }T=\Delta U$

(xiv) Specific heat in terms of degree of freedom:

(a) $C_{\mathrm{V}}=\frac{f}{2}R$
(b) $C_{\mathrm{P}}=\left(\frac{f}{2}+1\right)R$
(c) Ratio of $C_{\mathrm{P}}$ and $C_{\mathrm{V}}$ is $\gamma =\frac{C_{\mathrm{P}}}{C_{\mathrm{V}}}=1+\frac{2}{f}$
${\gamma }_{\mathrm{mono}}=\frac{5}{3}=1.6, {\gamma }_{\mathrm{di}}=\frac{7}{5}=1.4, {\gamma }_{\mathrm{tri}}=\frac{4}{3}=1.33$ at normal temperature.

(xv) Gaseous mixture:
Let ${\mu }_1$ moles of one gas is mixed with ${\mu }_2$ moles of another gas in a closed vessel, and $N_{\mathrm{A}}$ is Avogadro’s number, then

(a) Number of molecules of first gas $N_1={\mu }_1{N}_{\mathrm{A}}$ and number of molecules of the second gas $N_2={\mu }_2{N}_{\mathrm{A}}$
(b) Total mole fraction $\mu =\left({\mu }_1+{\mu }_2\right)$
(c) If M1 is the molecular weight of the first gas and M2 that of the second gas. Then the molecular weight of the mixture is 
M=μ1M1+μ2M2μ1+μ2
(d) Specific heat of the mixture at constant volume will be $C_{{\mathrm{V}}_{\mathrm{mix}}}=\frac{{\mu }_1{C}_{{\mathrm{V}}_1}+{\mu }_2{C}_{{\mathrm{V}}_2}}{{\mu }_1+{\mu }_2}=\frac{\left(\frac{m_1}{M_1}{C}_{{\mathrm{V}}_1}+\frac{m_2}{M_2}{C}_{{\mathrm{V}}_2}\right)}{\left(\frac{m_1}{M_1}+\frac{m_2}{M_2}\right)}$.
(e) Specific heat of the mixture at constant pressure will be
$C_{{\mathrm{P}}_{\mathrm{mix}}}=\frac{{\mu }_1{C}_{{\mathrm{P}}_1}+{\mu }_2{C}_{{\mathrm{P}}_2}}{{\mu }_1+{\mu }_2}=\frac{R}{{\mu }_1+{\mu }_2}\left[{\mu }_1\left(\frac{{\gamma }_1}{{\gamma }_1-1}\right)+{\mu }_2\left(\frac{{\gamma }_2}{{\gamma }_2-1}\right)\right]$$$

(f) ${\gamma }_{\mathrm{mix}}=\frac{C_{{\mathrm{P}}_{\mathrm{mix}}}}{C_{{\mathrm{V}}_{\mathrm{mix}}}}=\frac{{\mu }_1{C}_{{\mathrm{P}}_1}+{\mu }_2{C}_{{\mathrm{P}}_2}}{{\mu }_1{C}_{{\mathrm{V}}_1}+{\mu }_2{C}_{{\mathrm{V}}_2}}=\frac{{\mu }_1{\gamma }_1\left({\gamma }_2-1\right)+{\mu }_2{\gamma }_2\left({\gamma }_1-1\right)}{{\mu }_1\left({\gamma }_2-1\right)+{\mu }_2\left({\gamma }_1-1\right)}$