HARD
Earn 100
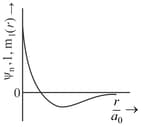
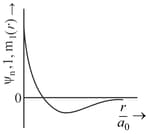
Which of the following graphs of radial part of wave-function versus distance from nucleus is/are correctly labelled?
(a)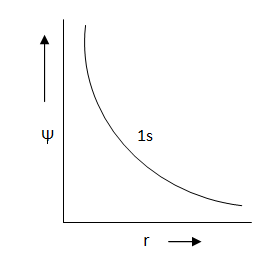

(b)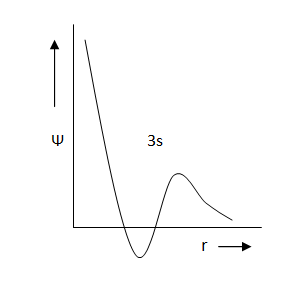

(c)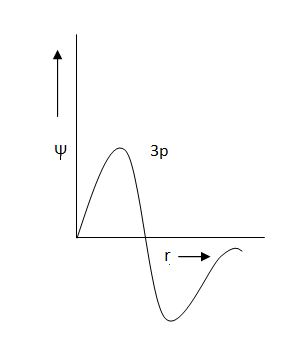

(d)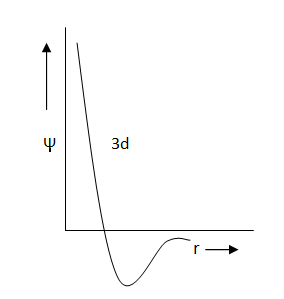

50% studentsanswered this correctly
Important Questions on Structure of Atom
MEDIUM
MEDIUM
EASY
MEDIUM
The wavelength (in ) of a particle of mass moving with a velocity of is ______
MEDIUM
MEDIUM
EASY
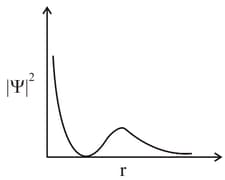
HARD
HARD
| Column – 1 | Column – 2 | Column – 3 |
| (I) orbital | (i) |
(P) |
| (II) orbital | (ii) One radial node | (Q) Probability density at nucleus |
| (III) orbital | (iii) | (R) Probability density is maximum at nucleus |
| (IV) orbital | (iv) -plane is a nodal plane | (S) Energy needed to excite an electron from state to state is times the energy needed to excite electron from state to state. |
HARD
| Column 1 | Column 2 | Column 3 |
| (I) orbital | (i) |
(P) |
| (II) orbital | (ii) One radial node | (Q) Probability density at the nucleus . |
| (III) orbital | (iii) | (R) Probability density is maximum at the nucleus. |
| (IV) orbital | (iv) -plane is a nodal plane | (S) Energy needed to excite an electron from state to state is times the energy needed to excite are electron from state to state. |
EASY
MEDIUM
EASY
MEDIUM
HARD
The correct plot for orbital is :
MEDIUM
A source of monochromatic radiation wavelength provides of energy in seconds. When this radiation falls on the surface of sodium, electrons are ejected per second. Assume that wavelength is sufficient for ejection of electron from the surface of sodium metal. The value of is ______. (Nearest integer)
MEDIUM
The wavelength of electrons accelerated from rest through a potential difference of is The value of is. (Nearest integer)
Given: Mass of electron
Charge on an electron
Planck's constant
MEDIUM
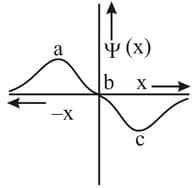
MEDIUM
[Planck's constant ]
MEDIUM