EASY

Earn 100

Why acceleration is zero when velocity is maximum in SHM?

Important Questions on Oscillations

HARD

Physics>Waves and Oscillations>Oscillations>Phase of S.H.M

A particle of mass

m

is attached to one end of a massless spring of force constant

k

, lying on a frictionless horizontal plane. The other end of the spring is fixed. The particle starts moving horizontally from its equilibrium position at time

t = 0

with an initial velocity

u_{0}

. When the speed of the particle is

0.5 u_{0}

, it collides elastically with a rigid wall. After this collision :

MEDIUM

Physics>Waves and Oscillations>Oscillations>Phase of S.H.M

A light balloon filled with helium of density,

ρ_{H e}

is tied to a long light string of length,

l

and the string is attached to the ground. If the balloon is displaced slightly in the horizontal direction from the equilibrium and released then.

MEDIUM

Physics>Waves and Oscillations>Oscillations>Phase of S.H.M

Many random snapshots using a camera are taken of a particle in simple harmonic motion between,

x = - x_{0}

and

x = + x_{0}

with origin

x = 0

as the mean position. A histogram of the total number of times the particle is recorded about a given position (event no) would most closely resemble,

EASY

Physics>Waves and Oscillations>Oscillations>Phase of S.H.M

The radius of circle, the period of revolution, initial position and sense of revolution are indicated in the figure.
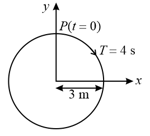
Question Image

y

-projection of the radius vector of rotating particle

P

MEDIUM

Physics>Waves and Oscillations>Oscillations>Phase of S.H.M

The position co-ordinates of a particle moving in a $3 D$ coordinate system is given by

$x = a \cos ω t$

$y = a \sin ω t$

and $z = a ω t$

The speed of the particle is:

MEDIUM

Physics>Waves and Oscillations>Oscillations>Phase of S.H.M

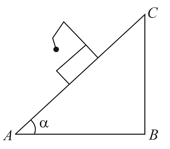
A simple pendulum is attached to a block which slides without friction down an inclined plane $(A B C)$ having an angle of inclination $α$ as shown while the block is sliding down the pendulum oscillates in such a way that at its mean position the direction of the string is,

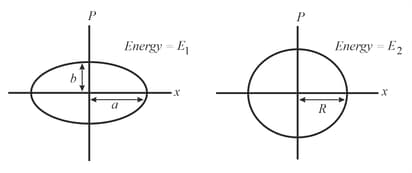
Question Image

HARD

Physics>Waves and Oscillations>Oscillations>Phase of S.H.M

A particle performs linear SHM. At a particular instant, the velocity of the particle is

u

and acceleration is

α

(both having the same direction). At another instant velocity is

v

and acceleration is

β (0 < α < β)

(both in opposite direction to each other).The distance between the two positions is

HARD

Physics>Waves and Oscillations>Oscillations>Phase of S.H.M

Two independent harmonic oscillators of equal mass are oscillating about the origin with angular frequencies

ω_{1}

and

ω_{2}

and have total energies

E_{1}

and

E_{2}

, respectively. The variations of their momenta

p

with positions

x

are shown in the figures. If

\frac{a}{b} = n^{2}

and

\frac{a}{R} = n

, then the correct equation(s) is (are)

Question Image

HARD

Physics>Waves and Oscillations>Oscillations>Phase of S.H.M

A particle moves with simple harmonic motion in a straight line. In first

τ s

, after starting from rest it travels a distance a, and in next

τ s

it travels 2a, in same direction, then :

EASY

Physics>Waves and Oscillations>Oscillations>Phase of S.H.M

Which of the following plots represents schematically the dependence of the time period of a pendulum if measured and plotted as a function of its oscillations? (Note: amplitude need not be small)

EASY

Physics>Waves and Oscillations>Oscillations>Phase of S.H.M

A particle executes linear simple harmonic motion with an amplitude of 3 cm. When the particle is at 2 cm from the mean position, the magnitude of its velocity is equal to that of its acceleration. Then its time period in seconds is

HARD

Physics>Waves and Oscillations>Oscillations>Phase of S.H.M

When a particle executes simple Harmonic motion, the nature of graph of velocity as function of displacement will be

HARD

Physics>Waves and Oscillations>Oscillations>Phase of S.H.M

A simple pendulum of length $l$ is made to oscillate with amplitude of $45$ degrees. The acceleration due to gravity is $g$ . Let $T_{0} = 2 π \sqrt{\frac{l}{g}} .$ The time period of oscillation of this pendulum will be

EASY

Physics>Waves and Oscillations>Oscillations>Phase of S.H.M

The oscillation of a body on a smooth horizontal surface is represented by the equation,

X = A \cos (ω t)

, where

X =

displacement at time

t

ω =

frequency of oscillation,

a =

acceleration at time

t

and

T =

time period.
Which one of the following graph shows correctly the variation

a

with

t

MEDIUM

Physics>Waves and Oscillations>Oscillations>Phase of S.H.M

A particle moves according to the law,

x = r c o s \frac{π t}{2}

. The distance covered by it the time interval between

t = 0 t o t = 3 s

MEDIUM

Physics>Waves and Oscillations>Oscillations>Phase of S.H.M

Two particles are performing simple harmonic motion in a straight line about the same equilibrium point. The amplitude and time period for both particles are same and equal to

A

and

T

, respectively. At time

t = 0

one particle has displacement

A

while the other one has displacement

- \frac{A}{2}

and they are moving towards each other. If they cross each other at time

t

, then

t

is:

MEDIUM

Physics>Waves and Oscillations>Oscillations>Phase of S.H.M

A particle performs simple harmonic motion with amplitude A. Its speed is tripled at the instant that it is at a distance

\frac{2 A}{3}

from equilibrium position. The new amplitude of the motion is:

EASY

Physics>Waves and Oscillations>Oscillations>Phase of S.H.M

A particle is executing SHM along a straight line. Its velocities at distances

x_{1}

and

x_{2}

from the mean position are

V_{1}

and

V_{2}

respectively. Its time period is:

HARD

Physics>Waves and Oscillations>Oscillations>Phase of S.H.M

A particle executes simple harmonic motion with an amplitude of

5 cm

. When the particle is at

4 cm

from the mean position, the magnitude of its velocity in

SI

units is equal to that of its acceleration. Then, its periodic time in seconds is:

EASY

Physics>Waves and Oscillations>Oscillations>Phase of S.H.M

When a particle executes SHM, the nature of graphical representation of velocity as a function of displacement is:

Why acceleration is zero when velocity is maximum in SHM?

Important Questions on Oscillations

Learn and Prepare for any exam you want !