Quadratic Graphs

Draw the graph of $x^2+x-12=0$ and state the nature of their solution.

Which of the following is not the graph of a quadratic polynomial of degree $2$?

What can you say about the quadratic polynomial represented by the graph

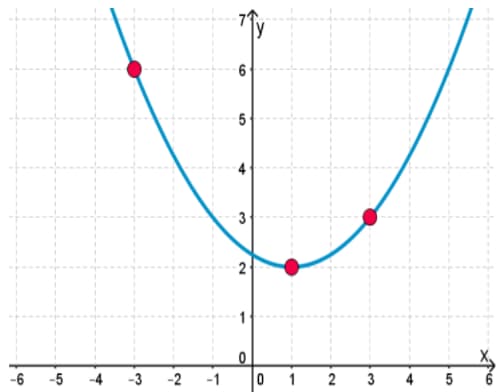
What can you say about the quadratic polynomial represented by the graph

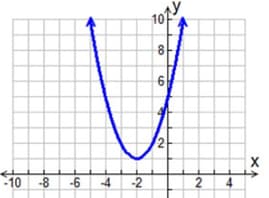
Identify the number of real roots of the quadratic polynomial represented by the graph

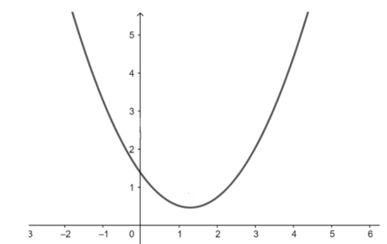
The graph of quadratic polynomial $f\left(x\right)=-3x^2+2x-2$ lies entirely below the $x$-axis.

Find the co-ordinates of a point on the parabola $y^2=12x$, whose ordinate is twice of its abscissa.

Prove that the curve whose polar equation is $r {\cos }^2\frac{\theta }{2}=1$ is a parabola.

$\mathrm{P}\left(2t, t^2\right)$ is a moving point. Find the locus of $P$. 

Find the co-ordinates of vertex and the length of latus rectum of the parabola $4y^2+4y+3x-2=0$

Find the locus of the point $(x, y)$ where $x=2t^2+3y=4t+5, t$ being a parameter.

Prove that the locus of the centre of a circle which has an intercept of a given length $2a$ on the axis of $x$ and passes through a given point on the $y$-axis at distance $b$ from the origin is the parabola $x^2-2by+b^2=a^2$.

Find the co-ordinates of the vertex, focus and the length of the latus-rectum of $y=x \tan \alpha -\frac{g{x}^2}{2u^2 {\cos }^2 \alpha }$.

Find the equation of the axis of the parabola $x^2-3y-6x+6=0$.

$P{P}^{\text{'}}$ is a double ordinate of the parabola $y^2=4ax$. Find the locus of its points of trisection.

The co-ordinates of vertex and focus of a parabola are $\left(2, 3\right)$ and $\left(2, -1\right)$ respectively. Show that the equation of the parabola is $x^2-4x+16y=44$.

If the equations of the axis and the directrix of a parabola are respectively $y-3=0$ and $x+3=0$ and if the length of its latus-rectum is $8$ unit, find the equation and the co-ordinates of the vertex of the parabola.

A point is moving in such a way that its distance from the straight line $2x+4y-3=0$ is always equal to its distance from the fixed point $\left(2, 5\right)$. Find the locus of the point. Identify the nature of the locus.

The area of the triangle formed by the tangents at $\left(x_1,y_1\right), \left(x_2,y_2\right)$and $\left(x_3,y_3\right)$ to the parabola $y^2=4ax(a>0)$ is

Let $a, b, c, d$ be distinct real numbers such that $a, b$ are roots of $x^2-5cx-6d=0,$ and $c, d$ are roots of $x^2-5ax-6b=0.$ Then $b+d$ is