Relations

Assertion $\left(\mathrm{A}\right)$: Domain and range of a relation $R=\left\{\left(x,y\right):x-3y=0\right\}$ defined on the set $\mathrm{A}=\left\{1,2,3\right\}$ are respectively $\left\{1,2,3\right\} \mathrm{and} \left\{2,4,6\right\}$.

Reason $\left(\mathrm{R}\right)$: Domain and Range of a relation $\mathrm{R}$ are respectively the sets $\left\{a:a\in A \mathrm{and} \left(a,b\right)\in R\right\} \mathrm{and} \left\{b:b\in A \mathrm{and} \left(a,b\right)\in R\right\}$

Let $n\left(A\right)=m$ and $n\left(B\right)=n$, then the total number of non-empty relations that can be defined from $A$ to $B$ is:

Let $A=\left\{1, 2\right\}$ and $B=\left\{3, 4\right\}$. Find the number of relations from $A$ to $B$.

Let $R$ be a relation from $Q$ to $Q$ defined by $R=\{\left(a, b\right):a, b\in Q$ and $a-b\in Z\}$. Show that, $\left(a, b\right)\in R$ and $\left(b, c\right)\in R$ implies that $\left(a, c\right)\in R$.

Let $R$ be a relation from $Q$ to $Q$ defined by $R=\{\left(a, b\right):a, b\in Q$ and $a-b\in Z\}$. Show that, $\left(a, b\right)\in R$ implies that $\left(b, a\right)\in R$.

The figure given below shows a relation between the sets $P$ and $Q$. Write this relation in roster form. What is its domain and range?

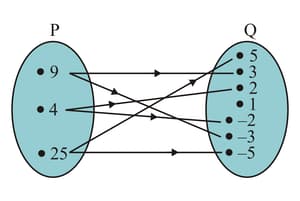
Let $A=\left\{1, 2, 3, 4, 5, 6\right\}$. Define a relation $R$ from $A$ to $A$ by $R=\left\{\left(x, y\right):y=x+1\right\}$. Write down the domain, codomain and range of $R$.

Let $\mathrm{A}=\left\{2, 4, 6\right\}$ and $\mathrm{B}=\left\{3, 4, 5, 6, 7, 8\right\}$ and $\mathrm{R}$ be the relation 'is greater than' from $\mathrm{A} \mathrm{to} \mathrm{B}$ then write $\mathrm{R}$ as a set of ordered pairs also find its domain and range.

The relation R in the set $\left\{1,2,3\right\}$ given by $R=\left\{(1,3),(3,1)\right\}$ then R is 

What is the meaning of domain?

If $n\left(A\right)=2$ and $n\left(B\right)=3$, then write the total number of non empty relations that can be defined from $A$ to $B$

Let $A=\left\{x:x^2<26\text{ and} x\text{ is a prime number}\right\} \text{and} B=\left\{y:\left|y\right|⩽1 \text{and} y \text{is a whole number}\right\},t\text{hen the number of relations from} B\text{ to} A \text{will be}$

Consider the sets $A=\left\{1,3,4\right\}, B=\left\{5,6\right\}, C=\left\{5,6,7\right\}$

$\left[a\right]$ Verify that $A\times \left(B\cup C\right)=\left(A\times B\right)\cup \left(A\times C\right)$

$\left[b\right]$ Verify that $A\times \left(B\cap C\right)=\left(A\times B\right)\cap \left(A\times C\right)$

$\left[c\right]$ If $P=\left\{a,b\right\}$ then find $P\times P\times P$

Consider the sets $A=\left\{1,2,3\right\}$, $B=\left\{a,b,c\right\}$. Write the number of relations from $A$ to $B.$

If $\left(a,b\right)\in R$ such that $a^2+1=b$ where relation $R$ is subset of $A\times B,$ then the number of elements in range of relation $R$ $\left(\text{where} A=\left\{-1,0,1,2\right\} \text{and} B=\left\{1,2,3\right\}\right)$.

If $(a,b)\in R$ such that $a^2+1=b$ where relation $R$ is subset of $A\times B$, then number of elements in range of relation $R$ (where$A=\{-1,0,1,2\}\text{ and }B=\{1,2,3\}$.

What is relation and What are the types of relation?

Let $R$ be a relation from $Q$ to $Q$ defined by $R=\{\left(a, b\right):a, b\in Q$ and $a-b\in Z\}$. Show that, $\left(a, a\right)\in R$ for all $a\in Q$.

The figure given below shows a relation between the sets $P$ and $Q$. Write this relation in set-builder form. What is its domain and range?

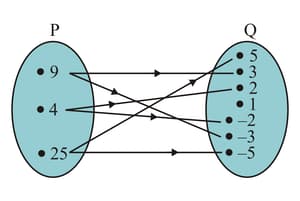
Let $A=\left\{1, 2, 3, 4, 5, 6\right\}$. Define a relation $R$ from $A$ to $A$ by $R=\left\{\left(x, y\right):y=x+1\right\}$. Depict this relation using an arrow diagram.