Pythagoras Theorem
Pythagoras Theorem: Overview
This Topic covers sub-topics such as Pythagoras Theorem, Right Angled Triangles, Distance between Two Points, Pythagorean Triplets, Pythagoras Property of Right Angle Triangles and, Application of Pythagorean Triplets in Geometry
Important Questions on Pythagoras Theorem
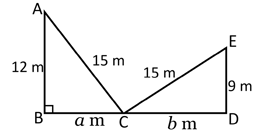
If length of is given as and
Use trigonometry to express in terms of . Hence show that .
If length of is given as and
Use the Pythagorean theorem to write two expressions for . Hence show that .
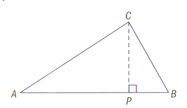
Label length as . Hence label length in terms of
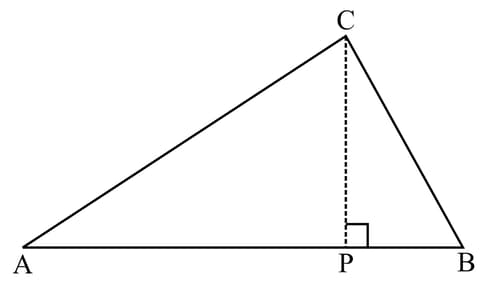
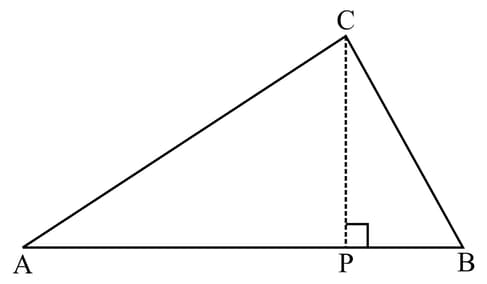
Copy the triangle with the altitude through meeting at right angles at point
Consider a right triangle, given below:
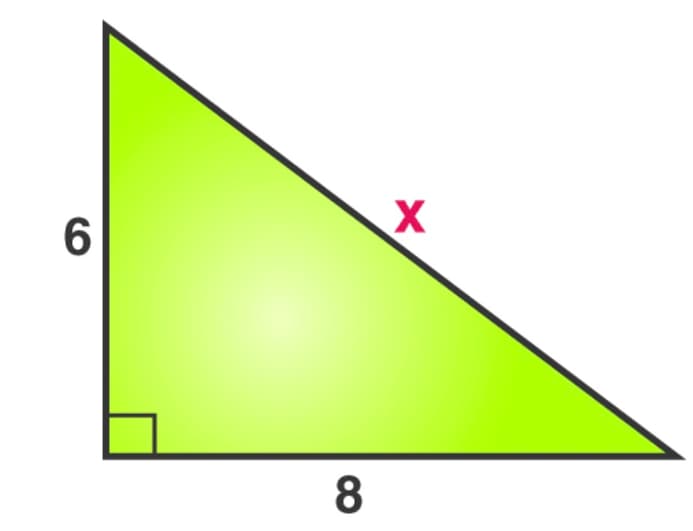
Find the value of .
The sum of acute angles in a right-angled triangle is always equal to _____.
A pole of height stands in front of a house of height . If the distance between the pole and the house is , then find the distance between their tops in .
Determine whether or not the triangles with the following sides are right-angled triangle:
Determine whether or not the triangles with the following sides are right-angled triangle:
Determine whether or not the triangles with the following sides are right-angled triangle:
Determine whether or not the triangles with the following sides are right-angled triangle:
Find the length of the unknown side in the following right-angled triangle. Round your answers to decimal point. [Enter the value excluding units]
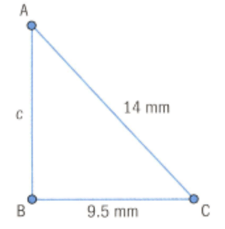
Find the length of the unknown side in the following right-angled triangle. Round your answers to decimal point. [Enter the value excluding units]
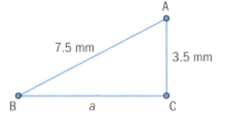
Find the length of the unknown side in the following right-angled triangle. Round your answers to decimal point. [Enter the value excluding units]
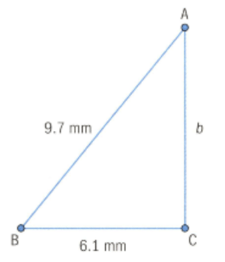
Find the length of the unknown side in the following right-angled triangle. Round your answers to decimal point. [Enter the value excluding units]
In is a point on such that . Then, the length of is
The hypotenuse of a right-angled triangle is and the ratio of its other two sides is . The length of the sides are
The distance between two pillars of heights and is . Find the distance of their tops in .
A ladder of length is leaning against a window which is from the ground. The ladder is placed on the window on the other side of the road which is from the ground. Find the breadth of the road in .