Hooke's Law and Modulus of Elasticity

A student performs an experiment to determine the Young’s modulus of a wire, exactly $2 \mathrm{m}$ long, by Searle’s method. In a particular reading, the student measures the extension in the length of the wire to be $0.8 \mathrm{mm}$ with an uncertainty of $\pm 0.05 \mathrm{mm}$ at a load of exactly $1.0 \mathrm{kg}$. The student also measures the diameter of the wire to be $0.4 \mathrm{mm}$ with an uncertainty of $\pm 0.01 \mathrm{mm}$. Take $g=9.8 \mathrm{m} {\mathrm{s}}^{-2}$ (exact). The Young’s modulus obtained from the reading is

Same tension is applied to the following four wires made of same material. The elongation is longest in

The bulk modulus of a liquid is $3\times {10}^{10}{\mathrm{Nm}}^{-2}$. The pressure required to reduce the volume of liquid by $2\%$ is :

A steel wire of cross-sectional area $3\times {10}^{-6} {\mathrm{m}}^2$ can withstand a maximum strain of ${10}^{-3}$. Young's modulus of steel is $2\times {10}^{11} \mathrm{N} {\mathrm{m}}^{-2}$. The maximum mass this wire can hold is,

A rod of length $1000 \mathrm{mm}$ and coefficient of linear expansion $\alpha ={10}^{-4}$ per degree is placed symmetrically between fixed walls separated by $1001 \mathrm{mm}$. Young's modulus of the rod is ${10}^{11}\mathrm{N} {\mathrm{m}}^{-2}$. If the temperature is increased by $20°\mathrm{C},$ then the stress developed in the rod is (in $\mathrm{N} {\mathrm{m}}^2$)

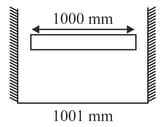
The backlash error can be eliminated in Searle's experiment, by rotating screw in

The translational kinetic energy of $1 \mathrm{g}$ molecule of a gas, at temperature $300 \mathrm{K}$ is $\left(R=8.31 \mathrm{J} {\mathrm{mol}}^{-1} {\mathrm{K}}^{-1}\right)$

A copper and a steel wire of same diameter are connected end to end. A deforming force $F$ is applied to this composite wire which causes a total elongation of $1$ $\mathrm{cm}$. The two wires will have:

The area of cross-section of a wire of length $2.1 \mathrm{m}$ is $2{ \mathrm{mm}}^2.$ Find the increase in its length when it is loaded with $0.5 \mathrm{kg}.$ The Young's Modulus of material of wire is $11\times {10}^{10} \mathrm{N}·{\mathrm{m}}^{-2}.$ $\left(g=10 \mathrm{m}{ \mathrm{s}}^{-2}\right)$

A wire of length $\text{'}L\text{'}$ suspended vertically from a rigid support is made to suffer extension $\text{'}l\text{'}$ in its length by applying a force $\text{'}F\text{'}.$ Then the work done is $\underline{ }$

The length of a rod under longitudinal tension $T_1$ is $L_1$ and that under longitudinal tension$T_2$ is $L_2$. What is the actual length of the rod, in the absence of tensions?

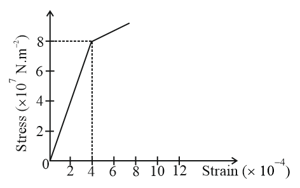
Find the Young's modulus of the wire whose stress-strain curve is as shown in the following figure:

One end of a wire of $8 \mathrm{mm}$ radius and $100 \mathrm{cm}$ length is fixed and the other end is twisted through an angle of $45°,$ The angle of shear is

The ratio of shearing stress to the corresponding shearing strain is called the modulus of _____.

The dimensional formula of modulus of rigidity is $M{L}^{-1}{T}^{-2}$.

State the units and dimensions of modulus of rigidity. 

The dimensional formula of modulus of rigidity is

A rubber ball is taken to a $100 \mathrm{m}$ deep lake and its volume changes by $0.1\%$. The bulk modulus of rubber is nearly

A steel rail of length $5 \mathrm{m}$ and area of cross-section $40\mathrm{ }{\mathrm{cm}}^2$ is prevented from expanding along its length while the temperature rises by $10 °\mathrm{C}$ . If coefficient of linear expansion and Young's modulus of steel are $1.2\times {10}^{-5}\mathrm{ }{\mathrm{K}}^{-1}$ and $2\times {10}^{11}\mathrm{ }\mathrm{N} {\mathrm{m}}^{-2}$ respectively, the force developed in the rail is approximately:

The pressure that has to be applied to the ends of a steel wire of length 10 cm to keep its length constant when its temperature is raised by 100^oC is :
(For steel Young's modulus is 2 x 10¹¹ N m^-2 and coefficient of thermal expansion is 1.1 x 10^-5 K^-1)