Velocity and Acceleration in Simple Harmonic Motion

A particle performs S.H.M. with amplitude $A$. The speed of particle is doubled at the instant when it is at $\frac{A}{2}$distance from mean position. The new amplitude of the motion is

The $x-t$ graph of a particle performing simple harmonic motion is shown in the figure. The acceleration of the particle at $t=2 \mathrm{s}$ is:

If velocity of body is half the maximum velocity. Then what is the distance from the mean position?

 Two particles P and Q of equal masses are suspended from two massless springs of force constants $k_1$ and $k_2$ respectively. If maximum velocities during oscillation are equal then the ratio of amplitudes of P and Q is

If the maximum velocity of a particle performing S.H.M. is $v$, then the average velocity during its motion from one extreme position to the other will be 

Velocity of a particle moving along a straight line at any time $t$ is given by $v=\cos \left(\frac{\pi }{3}t\right)$. Find out the distance travelled by the particle in the first two seconds.

A body is executing simple harmonic motion. At time $t$, the positon and acceleration of the body are $x\left(t\right)=x_0 \mathrm{m}$ and $a\left(t\right)=a_0 \mathrm{m} {\mathrm{s}}^{-2}$, respectively. If $x_0=a_0$, then the angular velocity (in $\mathrm{rad} {\mathrm{s}}^{-1}$)

A hydrometer executes simple harmonic motion when it is pushed down vertically in a liquid of density $\rho$. If the mass of hydrometer is $\mathrm{m}$ and the radius of the hydrometer tube is $r$, then the time period of oscillation is

The ratio of the magnitudes of maximum acceleration to the corresponding velocity of a body undergoing simple harmonic motion, $x=a\sin 2\pi ft$ is

The velocity of a particle executing SHM, while passing from its mean position is $V_0$. If its amplitude is doubled, without changing its period of oscillation, its velocity at the mean position will be

A body starts moving on $x$-axis from rest from $x=-2\mathrm{m}$. Acceleration $\overrightarrow{\mathrm{a}}$ of the particle varies according to the equation

$\overrightarrow{a}=-{\left(\pi \mathrm{rad} {\mathrm{s}}^{-1}\right)}^2\left(\overrightarrow{x}\right)$ for $0\le t\le \frac{1}{2}\mathrm{s}$

$\overrightarrow{a}=\left(5\pi \mathrm{m} {\mathrm{s}}^{-2}\right)\left(\hat{x}\right)$ for, $t>\frac{1}{2} \mathrm{s}$

Where $\overrightarrow{x}$ is the position vector of the particle at any instant $t$. Then velocity of the particle at $\mathrm{x}=\frac{\pi }{2} \mathrm{m}$ is

Figure shows the graph of velocity versus displacement of particle executing simple harmonic motion. The frequency of oscillation of the particle will be

If $y=A\sin \left(kx-\omega t\right)$, then find $\frac{{\displaystyle \frac{dy}{dx}}}{{\displaystyle \frac{dy}{dt}}}$.

The velocity of a particle, executing S.H.M, is at its mean position.

The displacement of two particles executing S.H.M are represented by $y_1=a\sin \omega t$ and $y_2=a\cos \left(\omega t+\varphi \right)$. The phase difference between the velocities of these particles is

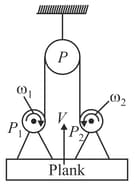
In the figure shown two motors $P_1 \& P_2$ fixed on a plank which is hanging with light string passing over fixed Pulley $P$. If the motors starts winding the thread with angular velocity ${\omega }_1$ & ${\omega }_2$ then velocity of plank $V$ is (here $R_1 \& R_2$ are the radii of motor rotor respectively) [Given: ${\omega }_1=2 \mathrm{rad} {\mathrm{s}}^{-1}, R_1=2 \mathrm{m}, {\omega }_2=2 \mathrm{rad} {\mathrm{s}}^{-1}, R_2=3 \mathrm{m}$]

Which one of the following is the correct acceleration vs. time graph for a particle performing SHM?

Which one of the following is the correct graph for acceleration vs. displacement of a particle performing SHM?

The shape of velocity vs. time graph for a particle performing SHM is

A particle performs simple harmonic motion. A large number of snapshots of its position are taken at random. A histogram of these positions will