Banking of Roads

Which force is applied to the well of death?

What is well of death?

Why a cyclist lean inwards when negotiating a curve?

Why out side of road is raised at the turning? 

Obtain an expression for the maximum speed with which a vehicle can safely negotiate a curved rough road banked at an  angle $\theta$.

A car is moving on a circular road of radius $150 \mathrm{m}$ with a coefficient of friction $0.6$. With what optimum velocity should the car be moved so that it crosses the turn safely.:

A circular track of radius $400 \mathrm{m}$ is banked at an angle of$10°$ . If the coefficient of friction between the tyre of a car and the track is $0.2$, what is the,

(a) optimum speed of the car to avoid the wear and tear on its tyre, and 

(b) Maximum permissible speed to avoid slipping.

If a car moves on a circular banked road the centripetal force may be provided by :-

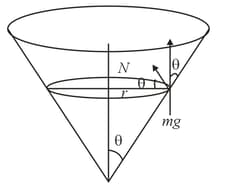
A particle describes a horizontal circle of radius r in a funnel type vessel of frictionless surface with half one angle $\theta$ (as shown in figure). If mass of the particle is m, then in dynamical equilibrium the speed of the particle must be –

What is the minimum speed a car can travel on an inclined road in terms of radius of the curved path $R$, acceleration due to gravity $g$, coefficient of static friction ${\mu }_s$, and the inclined angle of the road?

When moving on an circular inclined road slowly, friction prevents the vehicle from sliding inside the circular path.

When a car is moving in minimum speed on an inclined path, what will be the direction of friction between the wheels and the road?

A particle is moving in a circular path due to the action of a central attractive force which is inversely proportional to the distance $r$. Find the speed of the  particle.

The minimum and maximum distances of a satellite from the centre of the earth are $2R$ and $4R$ respectively, where $R$ is the radius of the earth and $M$ is the mass of the Earth. The radius of curvature at the point of minimum distance is

A car is negotiating a curved road of radius R. The road is banked at an angle $\mathrm{\theta }$ . The coefficient of friction between the tyres of the car and the road is ${\mathrm{\mu }}_{\mathrm{s}}$ . The maximum safe velocity on this road is:

STATEMENT-1 : A cyclist is cycling on a rough horizontal circular track with increasing speed. Then the net frictional force on cycle is always directed towards centre of the circular track.

STATEMENT-2 : For a particle moving in a circle, component of its acceleration towards centre, that is, centripetal acceleration should exist (except when speed is zero instantaneously).

A cyclist goes round a circular path of length 400 m in 20 s. calculate the angle through which he bends from vertical in order to maintain the balance

A body is revolving with a constant speed along a circle. If its direction of motion is reversed, but the speed remains the same, then,

If a curved road is banked at an angle ${\theta }_1$ the safe limit of the speed is $v_1$ . If the same road is banked at an angle ${\theta }_2$ , the safe limit of the velocity is $v_2$ . The ratio $v_1 :v_2$ is equal to