Rolling without Slipping

A disc of radius $0.1\mathrm{ }\mathrm{m}$ rolls without sliding on a horizontal surface with a velocity of $6\mathrm{ }\mathrm{m} {\mathrm{s}}^{-1}$ . It then ascends a smooth continuous track as shown in figure. The height upto which it will ascend is (in $\mathrm{cm}$) : ( $g=10\mathrm{ }{\mathrm{m} \mathrm{s}}^{-2}$ )

A ring of radius $2 \mathrm{m}$ weights $100 \mathrm{kg}.$ It rolls (pure rolling) along a horizontal floor so that its centre of mass has a speed of $20 \mathrm{cm} {\mathrm{s}}^{-1}$. If work done to stop it is $x \mathrm{J}$. Then $x$ will be

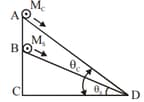
A cylinder of mass $M_{\mathrm{C}}$ and sphere of mass $M_{\mathrm{S}}$ are placed at points $A$and $B$of two inclines, respectively. (See Figure). If they roll on the incline without slipping such that their accelerations are the same, then the ratio $\frac{{\mathrm{sin\theta }}_{\mathrm{c}}}{{\mathrm{sin\theta }}_{\text{s}}}=\frac{2n+1}{2n}$. What is the value of $n$?

A uniform solid cylindrical roller of mass $m$ is being pulled on horizontal surface with force $F$ parallel to the surface applied at its centre. If the acceleration of the cylinder is $a$ and it is rolling without slipping, then the value of $F$ is

A uniform solid ball of mass '$m$' rolls without sliding on a fixed horizontal surface. The velocity of the lowest point of the ball with respect to the center of the ball is $v$. The total kinetic energy of the ball is:

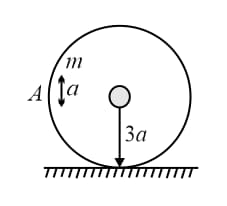
A ring of radius $3a$ is fixed rigidly on a table. A small ring whose mass is $m$ and radius $a$ rolls without slipping inside it as shown in the figure. The small ring is released from position $A$. When it reaches the lowest point, the speed of the centre of the ring at that time would be,

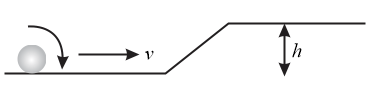
A small sphere rolls down without slipping from the top of a track in a vertical plane as shown. The track has an elevated section and a horizontal path. The horizontal part is $1.0 \mathrm{m}$ above the ground level and the top of the track is $2.4 \mathrm{m}$ above the ground. Find the distance on the ground with respect to a point $B$ where the sphere lands.

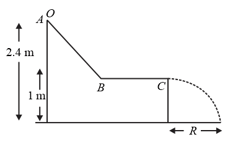
A solid sphere is rolling on a frictionless surface, as shown in figure with a translational velocity $v \mathrm{m} {\mathrm{s}}^{-1}$. If it has to climb the inclined surface, then $v$ should be

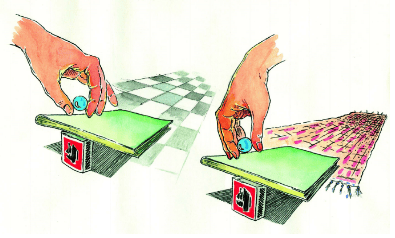
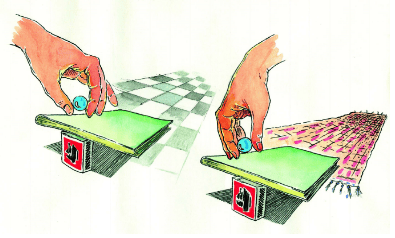
Roll the marble from different heights. Observe the effect on its movements.
Change the level of the slant of the book. Hold one end of the book with your hand and the other should touch the floor. Now, roll the marble from the end which is high to the plain floor. Mark with chalk, the place where the marble reaches. Conduct the same experiment by Changing the slope of the book each time.
Is there a relation between the slope of the book and the distance covered by the marble? 
 

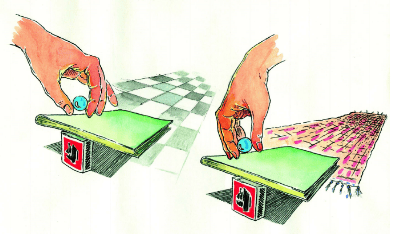
Roll the marble from different heights. Observe the effect on its movements.
Change the level of the slant of the book. Hold one end of the book with your hand and the other should touch the floor. Now, roll the marble from the end which is high to the plain floor. Mark with chalk, the place where the marble reaches. Conduct the same experiment by Changing the slope of the book each time.
The marble rolled at what height covers the longest distance?

Roll the marble from different heights. Observe the effect on its movements.
Change the level of the slant of the book. Hold one end of the book with your hand and the other should touch the floor. Now, roll the marble from the end which is high to the plain floor. Mark with chalk, the place where the marble reaches. Conduct the same experiment by Changing the slope of the book each time.
The marble rolled at what height covers the shortest distance?

A rod of uniform mass and of length $L$ can freely rotate in a vertical plane about an axis passing through $O.$ The angular velocity of the rod when it falls from position $P$ to $P^{\text{'}}$ through an angle $\alpha$ is

The ratio of the time taken by a solid sphere and that taken by a disc of the same mass and radius to roll down a rough inclined plane from rest from the same height is

A uniform solid sphere is released from the top point of an incline plane. If the incline surface is smooth the sphere takes a time $t_1$ to slide down. If the surface of incline is sufficient rough so that the sphere can roll without sliding the sphere takes time $t_2$ to roll down the same incline, $\frac{t_1}{t_2}$ will be :

In rotational motion of a rigid body, all particles move with _____.

A solid cylinder rolls without slipping down an inclined plane at an angle $60°$ with the horizontal. The acceleration of the cylinder is

Prove the result that the velocity $v$ of translation of a rolling body (like a ring, disc, cylinder or sphere) at the bottom of an inclined plane of a height $h$ is given by, $v^2=2gh/(1+k^2/R^2)$ using dynamical consideration (i.e., by consideration of forces and torques). Note k is the radius of gyration of the body.

Derive expression for velocity of a ring, solid cylinder and solid sphere having same radii rolling down the smooth inclined plane without slipping.

Deduce an expression for kinetic energy when a body is rolling on a plane surface without slipping.

What is the ratio of total kinetic energy and translation kinetic energy of rolling body of radius $\mathrm{R}$ and radius of gyration $\mathrm{k}$?