Pure Rolling

A disc of mass $M$ and radius $R$ rolls without slipping on a horizontal surface (see figure).

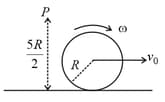
If the speed of its centre is $v_0$, then the magnitude of the angular momentum of the disc about a fixed point $P$ at a height $5\mathrm{R}/2$ above the horizontal surface

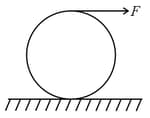
If a thin ring is subjected to a force $F$ as shown in the figure. Find the force of friction required to make sure that the ring does pure rolling on the rough surface.
 

A car starts from rest to cover a distance $s$. The coefficient of friction between the road and the tyres is $\mu$. The minimum time in which the car covers the distance is proportional to

A body rolls down without slipping on an inclined plane. The fractional of its total energy associated with rotation will be (radius of gyration is $k$ and radius of body is $R$)

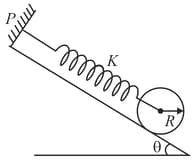
A uniform cylinder of mass $M$ and radius $R$ rolls without slipping down a slope of angle $\theta$ to the horizontal. The cylinder is connected to a spring constant $K$ while the other end of the spring is connected to rigid support at $P$. The cylinder is released when the spring is unstretched. The maximum displacement of the cylinder is

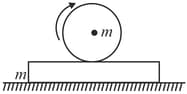
A uniform sphere of mass $m$ is given some angular velocity about a horizontal axis through its centre and gently placed on a plank of mass $m$. The coefficient of friction between the two is $\mu$. The plank rests on a smooth horizontal surface. The initial acceleration of the centre of the sphere relative to the plank will be:

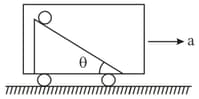
A smooth inclined plane fixed in a car accelerating on a horizontal road is shown in figure. The angle of incline $\theta$ is related to the acceleration a of the car as $a=g\tan \theta$. If the sphere is set in pure rolling on the incline

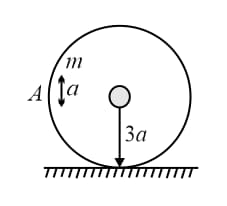
A uniform solid ball of mass '$m$' rolls without sliding on a fixed horizontal surface. The velocity of the lowest point of the ball with respect to the center of the ball is $v$. The total kinetic energy of the ball is:

A ring of radius $3a$ is fixed rigidly on a table. A small ring whose mass is $m$ and radius $a$ rolls without slipping inside it as shown in the figure. The small ring is released from position $A$. When it reaches the lowest point, the speed of the centre of the ring at that time would be,

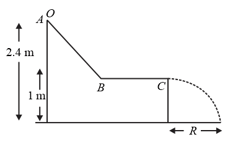
A small sphere rolls down without slipping from the top of a track in a vertical plane as shown. The track has an elevated section and a horizontal path. The horizontal part is $1.0 \mathrm{m}$ above the ground level and the top of the track is $2.4 \mathrm{m}$ above the ground. Find the distance on the ground with respect to a point $B$ where the sphere lands.

A solid sphere is rolling on a frictionless surface, as shown in figure with a translational velocity $v \mathrm{m} {\mathrm{s}}^{-1}$. If it has to climb the inclined surface, then $v$ should be

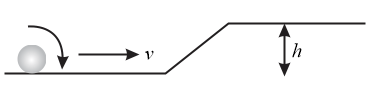
In the previous, which of the bodies reaches the ground with maximum rotational kinetic energy?

What is the work done against friction during rolling, if length of the incline is $1$ meter?

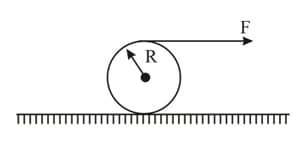
A ring of mass $m$ and radius $R$ is acted upon by a force $F$ as shown in the figure. There is sufficient friction between the ring and the ground. The force of friction necessary for pure rolling is

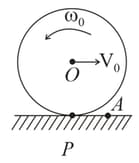
A hollow smooth uniform sphere A of mass $\text{'}m\text{'}$ rolls without sliding on a smooth horizontal surface. It collides elastically and head on with another stationary smooth solid sphere $B$ of the same mass $m$ and same radius. The ratio of kinetic energy of $\text{'}B\text{'}$ to that of $\text{'}A\text{'}$ just after the collision is :

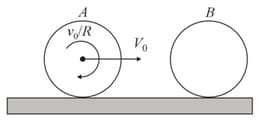
A uniform solid sphere of radius $r$ is released on a rough horizontal floor after imparting it an initial horizontal velocity vo and angular velocity ${\omega }_0$ as shown in the figure below. Coefficient of friction between sphere and ground is $\mu .$ What should be the relation between vo and $\omega 0$ so that the sphere comes to permanent rest after sometime?

A uniform solid sphere is released from the top point of an incline plane. If the incline surface is smooth the sphere takes a time $t_1$ to slide down. If the surface of incline is sufficient rough so that the sphere can roll without sliding the sphere takes time $t_2$ to roll down the same incline, $\frac{t_1}{t_2}$ will be :

In rotational motion of a rigid body, all particles move with _____.

A solid cylinder of mass $M$ and radius $R$ rolls down a smooth inclined plane about its own axis and reaches the bottom with velocity $v$. The height of the inclined plane is ($g=$ acceleration due to gravity)

A solid cylinder rolls without slipping down an inclined plane at an angle $60°$ with the horizontal. The acceleration of the cylinder is