X-ray Spectra, Characteristics Lines and Moseley's Law

For the production of characteristic kr− x-ray the electron transition is :

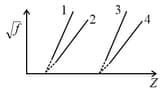
Which of the following plots will give a straight line, when a metal of atomic number $\mathrm{Z}$ is used to target a Coolidge tube. Let $\text{v}$ be the frequency of the ${\text{K}}_{\alpha }$ line. Given that corresponding values of $\mathrm{Z}$ and $\mathrm{v}$ are known for a number of metals. 

The properties of X-ray as put forward by Rontgen in his pioneering paper on the topic are as follows:

1. X-ray posses a very strong penetrative power. It can penetrate wood upto $3 \mathrm{cm}$ and an aluminium foil upto $15 \mathrm{mm} .$ If the hand is held between the discharge tube and the screen the dark shadow of the bones is visible within the slightly dark shadow of the hand.

2. Photographic plates and films "show themselves susceptible to X-rays." Hence, photography provides a valuable method of studying the effects of X-rays.
3. X-rays are neither reflected nor refracted (so far as Rontgen could discover). Hence, "X-rays cannot be concentrated by lenses."

4. X-rays discharge electrified bodies, whether the electrification is positive or negative.

5. X-rays are generated when the cathode rays of the discharge tube strike any solid body. A heavier element, such a's platinum, however, is much more efficient as a generator of X-rays than a lighter element, such as aluminium,

Most of Rontgen's observations stood the test of time, though some of them needed to be modified later. Now today we know if electron are accelerated through a potential difference $V,$ then maximum energy of emitted photon could be

 $E_{\max }=e V$
$\frac{h c}{\lambda_{\min }}=e V$
$\lambda_{\min }=\frac{h c}{e V}$

$\lambda_{\min }$ is also called cut off wavelength. Since electron may loose very small energy in a given collision, the upper value of $\lambda$ will approach infinity. When $\mathbf{X}$ -ray is produced in an X-ray tube, two types of X-ray spectra are observed : continuous spectra and line spectra.

A continuous spectrum is produced by bremsstrahlung, the electromagnetic radiation produced when free electrons are accelerated during collisions with ions. A line spectrum results when an electron having sufficient energy collides with a heavy atom, and an electron in an inner energy level is ejected from the atom. An electron from an outer energy level then fills the vacant inner energy level, resulting in emission of an X-ray photon.

The electron knocks out an inner shell electron of the atom with which it collides. Let us take a hypothetical case of a target atom whose $K$ -shell electron has been knocked out as shown.

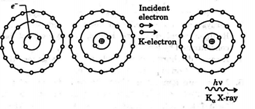
This will create a vacancy in $K$ -shell. Sensing this vacancy an electron from a higher energy state may make a transition to this vacant state. When such a transition takes place the difference of energy is converted into photon of electromagnetic radiation, which is called characteristic X-rays. Now depending upon the shell from which an electron makes a transition to $K$ -shell we may have different lines in the $K$ series of X-rays e.g., if electron from $L$ shell jumps to $K$ shell we have $K_{\alpha},$ if electron from $M$ shell jumps to $K$ shell we have $K_{\beta}$ X-ray and so on. Moseley conducted many experiments on characteristic X-rays, the findings of which played an important role in developing the concept of atomic number. Moseley's observations can be expressed as

$\sqrt{v}=a(Z-b)$

where $a$ and $b$ are constants. $Z$ is the atomic number of target atom and $n$ is the frequency.

Use the data given in the table shown to arrange the elements in the modern periodic table:

$K_{\alpha }$ wavelength emitted by an atom, of atomic number $Z=11\mathrm{}$ is  $1 \mathrm{\AA }$. Find the atomic number for an atom that emits $K_{\alpha }$ radiation with wavelength $4 \mathrm{\AA }$.

The X-ray wavelength ${\text{L}}_{\alpha }$ line of platinum ($Z=78$) is $1·30{\text{A}}^{\text{o}}\text{.}$ The X-ray wavelength of ${\mathit{\text{L}}}_{\alpha }$ line of Molybdenum ($Z=42$) is (constant $b=7.4$)

The atomic number (Z) of an element whose $k_a$ wavelength is $\lambda$ is 11. The atomic number of an element whose $k_a$ , wavelength is $4\lambda$ is equal to

In Mosley's equation, $\sqrt{v}=a\left(Z-b\right)$ , which was derived from the observations made during the bombardment of the metal target with $X$-rays

The wavelength of the ${\mathrm{k}}_{\mathrm{\alpha }}$ line for an element of atomic number 57 is $\mathrm{\lambda }$ . What is the wavelength of the ${\mathrm{K}}_{\mathrm{\alpha }}$ line for the element of atomic number 29?

The graph given below, shows the variation of $\sqrt{f}$ vs $z$ for characteristics X- rays. Lines 1,2,3 and 4 shown in the graph corresponds to any one of $K_{\mathrm{\alpha }}\mathrm{ }, K_{\mathrm{\beta }}\mathrm{ },\mathrm{ }{L}_{\mathrm{\alpha }}$ or $L_{\mathrm{\beta }}$ emission, then $L_{\mathrm{\beta }}$ is represented by ($f$ = frequency, $z$ = Atomic number)

X-rays are used in determining the molecular structure of crystaline because

$K_{\alpha }$ wavelength emitted by an atom of atomic number Z =11 is $\lambda .$Find the atomic number for an atom that emits $K_{\alpha }$ radiation with wavelength $4\lambda$

The $K_{\alpha }$ line obtained for molybdenum $(Z=42)$ is $0.71 \stackrel{\circ }{\mathrm{A}}$. Then, the wavelength of the $K_{\alpha }$ line of copper $(Z=29)$ is

The wavelengths of ${\text{K}}_{\alpha }$ $X$-rays of two metals $\mathrm{A}$ and $\mathrm{B}$ are $\frac{4}{1875\mathit{R}}$ and $\frac{1}{675\mathit{R}}$ respectively, where $R$ is Rydberg constant. The number of elements lying between $\mathrm{A}$ and $\mathrm{B}$ according to their atomic numbers is

$K_{\alpha }$ and $K_{\beta }$ $X-$rays are emitted when there is a transition of electron between the levels

When two different materials, $A$ and $B$ having atomic numbers, $Z_1$ and $Z_2$ are used as the target in Coolidge $\gamma$-ray tube at different operating voltage, $V_1$ and $V_2$, respectively, their spectrums are found as below.

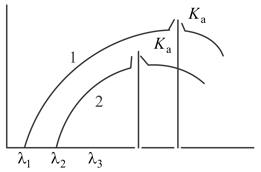
The correct relation is

When two different materials A and B having atomic number $Z_1$ and $Z_2$ are used as the target in Coolidge $\gamma$-ray tube at different operating voltage $V_1$ and $V_2$ respectively their spectrums are found as below.

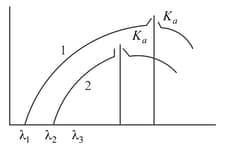
The correct relation is

When a metal of atomic number $Z$ is used as the target in a Coolidge tube. Let $v$ be the frequency of the $K_{\alpha }$ line. Corresponding values of $Z$ and $v$ are known for a number of metals. Which of the following plots will give a straight line?

Let ${\lambda }_{\alpha }$, ${\lambda }_{\beta }$ and ${\lambda }_{\alpha }^{\prime }$ denote the wavelengths of the X-rays of the $K_{\alpha }$, $K_{\beta }$ and $L_{\alpha }$ lines in the characteristic X-rays for a metal. Then,

Characteristic $X$-rays of frequency $4.2\times {10}^{18} \mathrm{Hz}$ are produced when transitions from $L$-shell to $K$-shell take place in a certain target material. Use Mosley’s law to determine the atomic number of the target material. Given Rydberg’s constant $R=1.1\times {10}^7 {\mathrm{m}}^{-1}$.