L.A.Sena Solutions for Chapter: Fundamentals of Mechanics, Exercise 1: Exercise
L.A.Sena Physics Solutions for Exercise - L.A.Sena Solutions for Chapter: Fundamentals of Mechanics, Exercise 1: Exercise
Attempt the practice questions on Chapter 1: Fundamentals of Mechanics, Exercise 1: Exercise with hints and solutions to strengthen your understanding. A Collection of Questions and problems in Physics solutions are prepared by Experienced Embibe Experts.
Questions from L.A.Sena Solutions for Chapter: Fundamentals of Mechanics, Exercise 1: Exercise with Hints & Solutions
A spacecraft is circling the earth along a circular orbit and retains its orientation with respect to the earth. Is zero gravity inside the spacecraft absolute in this case?
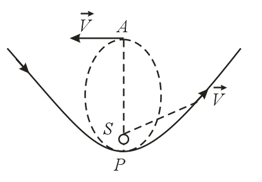
A comet flies into the solar system from remote outer space. The trajectory of the comet is a branch of a hyperbola. Can the comet become a satellite of the sun if the interaction of the comet with the planets of the solar system is ignored?
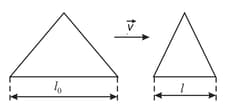
What shape will a round disk have if viewed from a system of coordinates with respect to which the disk is moving with a certain velocity directed along the diameter of the disk?
An isosceles right triangle is moving with respect to a system of coordinates with a velocity directed along the hypotenuse. When viewed from this system, the triangle appears to the an equilateral triangle. Find the velocity with which the triangle is moving with respect to this system.
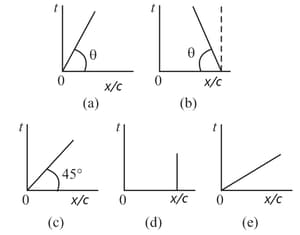
The various relationships that exist between time intervals, coordinates, and velocities in the special theory of relativity are conveniently illustrated via a system of coordinates in which on the axes we lay off either distance and time multiplied by the speed of light or time and distance divided by the speed of light. Curves that represent motion in such systems are known as world lines. Various world lines are shown in the figure in the vs. Coordinates. What does each line represent? Is there a line that contradicts the main principles of relativity theory?
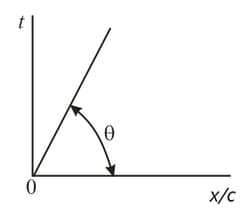
A world line is directed at an angle to the axis. What is the ratio of the kinetic energy calculated via the formula of relativity theory to the value calculated via the formula of classical mechanics? Take the specific case of as an example.
Two systems are moving with respect to each other with a certain velocity. The motion of one system in terms of the coordinates and of the other system is represented by a world line directed at an angle to the axis. After a time interval reckoned from the origin of coordinates has elapsed, one system sends a signal to the other. After what time will the second system receive the signal?
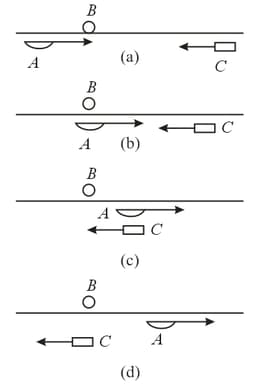
Three systems, and , are moving with respect to each other in such a manner that with respect to system the velocities of and coincide in magnitude and are directed towards (Figure (a)). When system comes alongside system (Figure (b)), the clocks in the two systems are synchronized. At this moment system begins emitting signals directed at and separated by equal time intervals . This continues until comes alongside (Figure (c)), with signals being set over the entire interval between the encounters. At this moment the clock in is synchronized with the clock in and system starts to send signals directed at that are separated by the same time intervals . Find the difference in readings of the clock in and when these two systems come alongside (Figure (d)).