Embibe Experts Solutions for Chapter: Area under Curves, Exercise 4: Exercise-4

Let $ABC$ be a triangle with vertices $A\left(6, 2\left(\sqrt{3}+1\right)\right), B\left(4, 2\right)$ and $C\left(8, 2\right).$ If $R$ be the region consisting of all these points and point $P$ inside $∆ABC$ which satisfy $d\left(P, BC\right)\ge$ max. $\left\{d\left(P, AB\right), d\left(P, AC\right)\right\}$ where $d\left(P ,L\right)$ denotes the distance of the point $P$ from the line $L.$ Sketch the region $R$ and find its area.

Find the area of the region which contains all the points satisfying the condition $|x-2y|+|x+2y|\le 8$ and $xy\ge 2.$

Find the area of the region which is inside the parabola $y=-x^2+6x-5,$ out side the parabola $y=-x^2+4x-3$ and left of the straight line $y=3 x-15.$

Consider the curve $C: y=\sin 2\mathrm{x}-\sqrt{3}\left|\sin x\right|,C$ cuts the $x$-axis at $\left(a,0\right), x\in \left(-\pi ,\pi \right)$

$A_1:$ The area bounded by the curve $C$ and the positive $x$-axis between the origin and the line $x=a.$

$A_2:$ The area bounded by the curve $C$ and the negative $x$-axis between the line $x=a$ and the origin. Prove that $A_1+A_2+8A_1{A}_2=4.$

Area bounded by the line $y=x,$ curve $y=f\left(x\right), \left(f\left(x\right)>x \forall x>1\right)$ and the lines $x=1, x=t$ is $t+\sqrt{1+t^2}-\left(1+\sqrt{2}\right)\forall t>1.$ Find $f\left(x\right)$ for $x>1.$

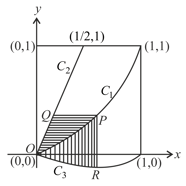
Let $C_1$ and $C_2$ be the graphs of the functions $y=x^2$ and $y=2x, 0\le x\le 1$ respectively. Let $C_3$ be the graph of a function $y=f\left(x\right), 0\le x\le 1, f\left(0\right)=0.$ For a point $P$ on $C_1,$ let the lines through $P,$ parallel to the axes, meet $C_2$ and $C_3$ at $Q$ and $R$ respectively (see figure).
If for every position of $P$ (on $C_1$), the areas of the shaded regions $OPQ$ and $ORP$ are equal, determine the function $f\left(x\right).$

Given the parabola $C:y=x^2$. If the circle centred at $y$-axis with radius $1$ touches parabola $C$ at two distinct points, then find the coordinate of the centre of the circle $K$ and the area of the figure surrounded by $C$ and $K$.

If $\left[\begin{array}{ccc}4a^2& 4a& 1\\ 4b^2& 4b& 1\\ 4c^2& 4c& 1\end{array}\right]\left[\begin{array}{c}f\left(-1\right)\\ f\left(1\right)\\ f\left(2\right)\end{array}\right]=\left[\begin{array}{l}3a^2+3a\\ 3b^2+3b\\ 3c^2+3c\end{array}\right], f\left(x\right)$ is a quadratic function and its maximum value occurs at a point $V.$ $A$ is a point of intersection of $y=f\left(x\right)$ with $x$ -axis and point $B$ is such that chord $AB$ subtends a right angle at $V.$ Find the area enclosed by $f\left(x\right)$ and chord $AB.$