Embibe Experts Solutions for Chapter: Atomic Physics, Exercise 4: Exercise - 4
Embibe Experts Physics Solutions for Exercise - Embibe Experts Solutions for Chapter: Atomic Physics, Exercise 4: Exercise - 4
Attempt the free practice questions on Chapter 33: Atomic Physics, Exercise 4: Exercise - 4 with hints and solutions to strengthen your understanding. Alpha Question Bank for Engineering: Physics solutions are prepared by Experienced Embibe Experts.
Questions from Embibe Experts Solutions for Chapter: Atomic Physics, Exercise 4: Exercise - 4 with Hints & Solutions
In a hydrogen like ionised atom, a single electron is orbiting around a stationary positive charge. If a spectral line of equal to is observed due to transition from to . What is the wavelength of a spectral line due to transition from to and also identify the element?
An electron in the ground state of hydrogen atoms is revolving in anti clock wise direction in a circular orbit of radius .
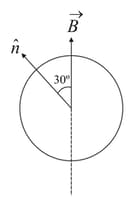
(i) Obtain an expression for the orbital magnetic dipole moment of the electron.
(ii) The atom is placed in a uniform magnetic induction, such that the plane normal to the electron orbit makes an angle of with the magnetic induction. Find the torque experienced by the orbiting electron.
A proton and an electron, both at rest initially, combine to form a hydrogen atom in the ground state. A single photon is emitted in this process. What is the wavelength?
A neutron of kinetic energy collides inelastically with a singly ionized helium atom at rest. It is scattered at an angle of with respect of its original direction.
(a) Find the allowed values of the energy of the neutron and that of the atom after the collision.
(b) If the atom gets de-excited subsequently by emitting radiation, find the frequencies of the emitted radiation. [Given: Mass of atom = (mass of neutrons Ionization energy of atom ]
Suppose the potential energy between electron and proton at a distance is given by , where and are positive constants. Use Bohr’s theory to obtain the energy of nth energy level for such an atom.
A positronium consists of an electron and a positron revolving about their common centre of mass. Derive and calculate
(i) Separation between the electron and positron in their first excited state.
(ii) Kinetic energy of the electron in ground state.
The ray of argon has a wavelength of . The minimum energy required to take out the outermost electron from argon atom is . Find the energy (in ) needed to knock out an electrons from the shell of an argon.
A schwarzschild black hole is characterized by its mass and a mathematical spherical surface of radius called the event horizon. If the radial distance of an object from the black hole is such that , then the object is “swallowed” by the black hole and rapidly decreased to the singular point
(a) Suppose a black hole of mass “captures” a proton to form a “black hole proton atom ” in circular orbit. Find the smallest radius of this atom.
(b) Obtain a numerical upper bound on such that a stable may exist.
(c) Find the minimum energy , in , required to dissociate this atom from the ground state.
(d) In , Stephen Hawking showed that quantum effects cause black to radiate like a black body with temperature . Discuss the possibility of the existence of the stable atom.
