Embibe Experts Solutions for Chapter: Centre of Mass, Momentum and Collisions, Exercise 1: Exercise - 1

A shell is fired from a canon with a velocity, $V$  at an angle $\theta$ with the horizontal direction. At the highest point in its path. it explodes into two pieces of equal masses. One of the pieces comes to rest. The speed of the other piece immediately after the explosion is

Two perfectly elastic balls of same mass m are moving with velocities $u_{1 }\mathrm{and} u_2.$ They collide head on elastically $n$ times. The kinetic energy of the system finally is:

A massive ball moving with speed $v$ collides head-on with a tiny ball at rest having a mass very less than the mass of the first ball. If the collision is elastic, then immediately after the impact, the second ball will move with a speed approximately equal to:

Ball $1$ collides head-on with an identical ball $2$ at rest. Velocity of the ball $2$after collision becomes two times that of the ball $1$after the collision. The coefficient of restitution between the two balls is:

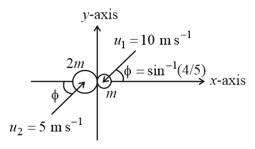
Two smooth spheres made of identical material have masses $m$ and $2m$ undergoes an oblique impact as shown in the figure. The initial velocities of the masses are also shown. The impact force is along the line joining their centres along the $x$-axis. The coefficient of restitution is $\frac{5}{9}$. The velocities of the masses after the impact and the approximate percentage loss in kinetic energy.

If the thrust force on a rocket is ejecting gases with a relative velocity of $300 \mathrm{m} {\mathrm{s}}^{-1},$ is $210 \text{N}$. Then the rate of combustion of the fuel will be:

A particle of mass $m$ at rest is acted upon by a force $F$ for a time $t$. Its kinetic energy after an interval $t$ is

A uniform rod having mass $m_1$ and length $L$ lies on a smooth horizontal surface. A particle of mass $m_2$ moving with speed $u$ on the horizontal surface strikes the free rod perpendicularly at an end and it sticks to the rod.

$\left(\mathrm{a}\right)$ Calculate the velocity of the centre of mass $C$ of the system constituting the rod plus the particle.

$\left(\mathrm{b}\right)$ Calculate the velocity of the particle with respect to $C$ before the collision.

$\left(\mathrm{c}\right)$ Calculate the velocity of the rod with respect to $C$ before the collision.

$\left(\mathrm{d}\right)$ Calculate the angular momentum of the particle and of the rod about the centre of mass $C$ before the collision.

$\left(\mathrm{e}\right)$ Calculate the moment of inertia of the rod plus particle about the vertical axis through the centre of mass $C$ after the collision.

$\left(\mathrm{f}\right)$ Calculate the velocity of the centre of mass $C$ and the angular velocity of the system about the centre of mass after the collision.