Embibe Experts Solutions for Chapter: Gravitation, Exercise 4: Exercise - 4
Embibe Experts Physics Solutions for Exercise - Embibe Experts Solutions for Chapter: Gravitation, Exercise 4: Exercise - 4
Attempt the free practice questions on Chapter 11: Gravitation, Exercise 4: Exercise - 4 with hints and solutions to strengthen your understanding. Alpha Question Bank for Engineering: Physics solutions are prepared by Experienced Embibe Experts.
Questions from Embibe Experts Solutions for Chapter: Gravitation, Exercise 4: Exercise - 4 with Hints & Solutions
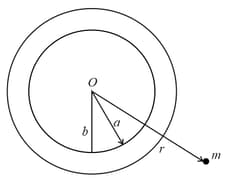
A sphere of density and radius has a concentric cavity of radius , as shown in the figure.
(a) Sketch the gravitational force exerted by the sphere on the particle of mass , located at a distance from the centre of the sphere as a function of r in the range
(b) Sketch the corresponding curve for the potential energy of the system.
(a) What is the escape speed for an object in the same orbit as that of earth around sun (take orbital radius ) but far from the earth? (Mass of the)
(b) If an object already has a speed equal to the earth’s orbital speed, what minimum additional speed must it be given to escape as in (a)?
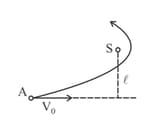
A cosmic body moves towards the sun with velocity (when far from the sun) and aiming parameter , the direction of the vector relative to the centre of the sun as shown in the figure. Find the minimum distance by which this body will get to the sun (mass of sun)
Two stars of mass and are in circular orbits around their centre of mass. The star of mass has an orbit of radius , the star of mass has an orbit of radius. (Assume that their centre of mass is not accelerating and distance between stars is fixed)
(a) Show that the ratio of the orbital radii of the two stars equals the reciprocal of the ratio of their masses, that is
(b) Explain why the two stars have the same orbital period and show that the period,
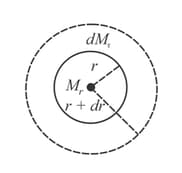
A star can be considered as a spherical ball of hot gas of radius. Inside the star, the density of the gas is at a radius and mass of the gas within this region is . The correct differential equation for variation of mass with respect to radius is (refer to the adjacent figure)
A star can be considered as a spherical ball of hot gas of radius . Inside the star, the density of the gas is at a radius and the mass of the gas within this region is . A star in its prime age is said to be under equilibrium due to gravitational pull and outward radiation pressure . Consider the shell of thickness . If the pressure on this shell is then the correct equation is ( is universal gravitational constant
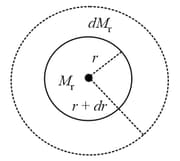
A star can be considered as a spherical ball of hot gas of radius . Inside the star, the density of the gas is at a radius and the mass of the gas within this region is . In astronomy order of magnitude, estimation plays an important role. The derivative be taken difference ratio Consider the star has a radius , pressure at its centre is and pressure at outer layer is zero if the average mass is and average radius then the expression for is
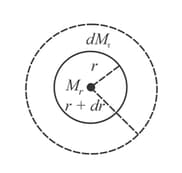
The value of mass and radius of sun are given by and , respectively. The pressure at the centre is about
