Embibe Experts Solutions for Chapter: Area under Curves, Exercise 4: EXERCISE-4

For what value of $\text{'}a\text{'}$ is the area of the figure bounded by $y=\frac{1}{x}, y=\frac{1}{2x-1}, x=2 \& x=a$ equal to $\ln \frac{4}{\sqrt{5}}$ sq. units $?$

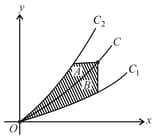
Let $C_1 \& C_2$  be two curves passing through the origin as shown in the figure. $A$ curve $C$ is said to "bisect the area" of the region between $C_1$ and $C_2,$ if for each point $P$ of $C,$ two shaded regions $A \& B$ shown in the figure have equal areas. Determine the upper curve $C_2,$ given that the bisecting curve $C$ has the equation $y=x^2$ and that the lower curve $C_1$ has the equation $y=\frac{x^2}{2}.$

Consider the curve $y=x^n$ where $n>1$ in the $1^{st}$quadrant. If the area bounded by the curve, the $x$-axis and the tangent line to the graph of $y=x^n$ at the point $\left(1, 1\right)$ is maximum, then find the value of $n.$

Consider the collection of all curves of the form $y=a-b{x}^2$ that pass through the point $\left(2, 1\right),$ where $a$ and $b$ are positive constants. Determine the value of $a$ and $b$ that will minimise the area of the region bounded by $y=a-b{x}^2$ and $x$-axis. Also find the minimum area.

Show that the area bounded by the curve $y=\frac{\ln x-c}{x},$ the $x$-axis and the vertical line through the maximum point of the curve is independent of the constant $c.$  Also find the area.

Let $f\left(x\right)$ be a continuos function given by $f\left(x\right)=\left\{\begin{array}{l}2x\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\mathrm{ }\mathrm{for} \left|x\right|\le 1\\ x^2+ax+b\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em} \mathrm{for} \left|x\right|>1\end{array}\right..$ Find the area of the region in the third quadrant bounded by the curves, $x=-2y^2$ and $y=f\left(x\right)$ lying on the left of the line $8x+1=0$

Find the value$\left(s\right)$ of parameter  $\text{'}a\text{'} \left(a>0\right)$ for each of which the area of the figure bounded by the straight line by $y=\frac{a^2-ax}{1+a^4} \&$  the parabola $y=\frac{x^2+2ax+3a^2}{1+a^4}$ is the greatest. 

Find the area bounded by $y=x+\sin x$ and its inverse between $x=0$ and $x=2\mathrm{\pi }$.