Embibe Experts Solutions for Chapter: Rotational Mechanics, Exercise 2: Exercise-2

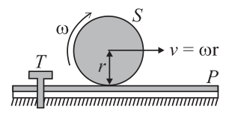
A sphere $S$ rolls without slipping, moving with a constant speed on a plank $P.$ The friction between the upper surface of $P$ and the sphere is sufficient to prevent slipping, while the lower surface of $P$ is smooth and rests on the ground. Initially, $P$ is fixed to the ground by a pin $T\mathit{.}$ If $T$ is suddenly removed-

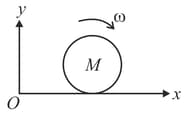
A disc of mass $M$ and radius $R$ is rolling with angular speed $\mathrm{\omega }$ on a horizontal plane as shown. The magnitude of angular momentum of the disc about the origin $O$ is:-

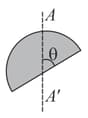
The moment of inertia of semicircular plate of radius $R$ and mass $M$ about axis $AA\mathit{\text{'}}$ in its plane passing through its centre is

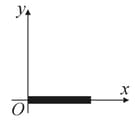
The figure shows a uniform rod lying along the $x$-axis. The locus of all the points lying on the $xy$-plane, about which the moment of inertia of the rod is same as that about $O$ is:

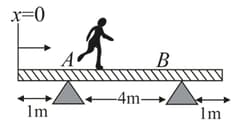
A man can move on a horizontal plank supported symmetrically as shown. The variation of normal reaction on support A with distance $x$ of the man from the end of the plank is best represented by

A disc of radius $R$ is rolling purely on a flat horizontal surface, with a constant angular velocity. The angle between the velocity and acceleration vectors of point $P$ is

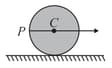
A ring of mass $m$ and radius $R$ has three particles attached to the ring as shown in the figure. The centre of the ring has a speed $v_0$. The kinetic energy of the system is : (slipping is absent)

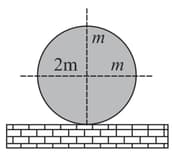
A solid sphere with a velocity (of centre of mass) $v$ and angular velocity $\omega$ is gently placed on a rough horizontal surface. The frictional force on the sphere