Embibe Experts Solutions for Chapter: Wave Motion on a String, Exercise 2: Exercise-2

A wave disturbance in a medium is described by $y\left(x,t\right)=0.02\cos \left(50\pi t+\frac{\pi }{2}\right)\cos \left(10\pi x\right)$, where $x$ and $y$ are in $\mathrm{metre}$ and$t$ is in $\mathrm{second}$:-

A string of length $L$ is stretched along the $x$ -axis and is rigidly clamped at its two ends. It undergoes transverse vibration. If $n$ is an integer, which of the following relations may represent the shape of the string at any time:-

A wave is propagating along $x$-axis. The displacement of particles of the medium in $z$-direction at $t=0$ is given by: $z=\exp \left[-{\left(x+2\right)}^2\right]$, where ' $x$ ' is in meter. At $t=1 \mathrm{s}$, the same wave disturbance is given by $z=\exp \left[-{\left(2-x\right)}^2\right]$. Then the wave propagation velocity is:-

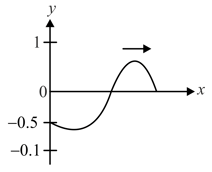
The equation of a wave travelling along the positive$x$-axis, as shown in figure at $t=0$ is given by:- 

For a sine wave passing through a medium, let$y$ be the displacement of a particle, $v$ be its velocity and a be its acceleration:-

$P,Q$ and $R$ are three particles of a medium which lie on the $x$-axis. A sine wave of wavelength $\lambda$ is travelling through the medium in the $x$-direction. $P$ and $Q$ always have the same speed, while $P$ and $R$ always have the same velocity. The minimum distance between:-

Sounds from two identical sources $S_1$ and $S_2$ reach a point $P$. When the sounds reach directly, and in the same phase, the intensity at $P$ is $I_0$. The power of $S_1$ is now reduced by $64\%$ and the phase difference between $S_1$ and $S_2$ is varied continuously. The maximum and minimum intensities recorded at $P$ are now $I_{\max }$ and $I_{\min }$ :-

Two audio speakers are kept some distance apart and are driven by the same amplifier system. A person is sitting at a place $6.0 \mathrm{m}$ from one of the speakers and $6.4 \mathrm{m}$ from the other. If the sound signal is continuously varied from $500 \mathrm{Hz}$ to $5000 \mathrm{Hz}$, then the frequencies for which there is a destructive interference at the place of the listener? Speed of sound in air $=320 \mathrm{m} {\mathrm{s}}^{-1}$.