Name: Power Transmitted by a Wave on a String
Uploaded: 2019-07-19
Duration: 7 min 4 s
Description: We know that a wave transfers energy from one point to another, but to find the power transmitted by a wave on a string, watch this video.

Question

The figure shows a snap photograph of a vibrating string at $t = 0$ . The particle $P$ is observed moving up with velocity $20 \sqrt{3} cm s^{- 1}$ . The tangent at $P$ makes an angle $60 °$ with $x$ -axis (i) Find the direction in which the wave is moving (ii) the equation of the wave (iii) the total energy carried by the wave per cycle of the string. [Assuming that $μ$ , the mass per unit length of the string $= 50 g m^{- 1}]$

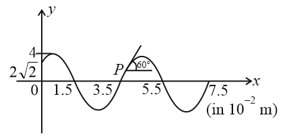
Question Image

Accepted Answer

(a) From the above figure, slope at a point $P$ is,

$\frac{d y}{d x} = \tan (60^{°}) = \sqrt{3}$ .

The given velocity of a particle at $P$ is,

$v_{p} = 20 \sqrt{3} cm s^{- 1} = 20 \sqrt{3} \times 10^{- 2} m s^{- 1}$ .

From relation,

$v_{p} = - v_{w} (\frac{d y}{d x})$ $. . . (1)$

Putting values in the equation $(1)$ ,

$20 \sqrt{3} \times 10^{- 2} = - v_{w} \sqrt{3} v_{w} = - 0.20 m s^{- 1} .$

From above, we get the velocity of wave as negative which means the wave is travelling in the direction of negative $x$ -axis.

(b) General equation of wave travelling in negative $x$ -axis is,

$y = A \sin (ω t + k x + ϕ)$ $. . . (1)$

Given:

$A = 4 \times 10^{- 3} m$

$λ = 4 \times 10^{- 2} m$

$k = \frac{2 π}{λ} = \frac{2 π}{4 \times 10^{- 2}} = 50 π radian m^{- 1}$

$ω = v_{w} k = 50 π \times 0.20 = 10 π radian s^{- 1}$

$μ = 50 g m^{- 1} = 0.05 kg m^{- 1}$ .

At $t = 0, x = 0, y = 2 \sqrt{2} \times 10^{- 3} m$ . Putting these values in equation $(1)$ ,

$2 \sqrt{2} \times 10^{- 3} = 4 \times 10^{- 3} \sin (ϕ) \sin (ϕ) = \frac{1}{\sqrt{2}} ϕ = \frac{π}{4}$

Putting above all values in equation $(1)$ ,

$y = (4 \times 10^{- 3}) \sin (10 π t + 50 π x + \frac{π}{4})$

(c) The energy carried per cycle,

$E = P T = \frac{P}{f} = 2 π^{2} A^{2} f μ ν$ $. . . (2)$

Putting values in the above equation $(2)$ ,

$E = 2 \times {(3.14)}^{2} \times {(4 \times 10^{- 2})}^{2} \times 5 \times 0.05 \times 0.20 = 1.6 \times 10^{- 5} J$ .

Embibe Experts Solutions for Chapter: Wave Motion on a String, Exercise 4: Exercise-4

Embibe Experts Physics Solutions for Exercise - Embibe Experts Solutions for Chapter: Wave Motion on a String, Exercise 4: Exercise-4

Questions from Embibe Experts Solutions for Chapter: Wave Motion on a String, Exercise 4: Exercise-4 with Hints & Solutions

Learn and Prepare for any exam you want !