D. C. Pandey Solutions for Chapter: Projectile Motion, Exercise 1: Excercise 1

The trajectory of a projectile near the surface of the earth is given as $y=2x-9x^2$. If it were launched at an angle ${\theta }_0$ with speed $v_0$, then (Take, $g=10 \mathrm{m} {\mathrm{s}}^{-2}$)

In a three-dimensional system, the position coordinates of a particle (in motion) are given below $x=a\cos \omega t, y=a\sin \omega t, z=a\omega t$. The velocity of the particle will be

A body is projected at $t=0$ with a velocity $10 \mathrm{m} {\mathrm{s}}^{-1}$ at an angle of $60°$ with the horizontal. The radius of curvature of its trajectory at $t=1 \mathrm{s}$ is $R$. Neglecting air resistance and taking acceleration due to gravity $g=10 \mathrm{m} {\mathrm{s}}^{-2}$, the value of $R$ is

A projectile is thrown in the upward direction making an angle of $60°$ with the horizontal with a velocity of $140 \mathrm{m} {\mathrm{s}}^{-1}.$ Then the time after which its velocity makes an angle $45°$ with the horizontal is (Acceleration due to gravity, $g=10 \mathrm{m} {\mathrm{s}}^{-2}$)

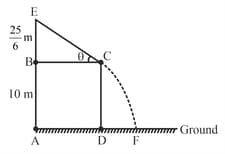
A rough inclined plane $BCE$ of height $\left(\frac{25}{6}\right) \mathrm{m}$ is kept on a rectangular wooden block $ABCD$ of height $10 \mathrm{m}$, as shown in the figure. A small block is allowed to slide down from the top $E$ of the inclined plane. The coefficient of kinetic friction between the block and the inclined plane is $\frac{1}{8}$ and the angle of inclination of the inclined plane is ${\sin }^{-1}\left(0.6\right)$. If the small block finally reaches the ground at a point $F$, then $DF$ will be (Acceleration due to gravity, $\mathrm{g}=10 \mathrm{m} {\mathrm{s}}^{-2}$)

​​​​​​​

Two boys conducted experiments on the projectile motion with a stopwatch and noted some readings. As one boy throws a stone in the air at the same angle as the horizontal, the other boy observes that after $4 \mathrm{s}$, the stone is moving at an angle $30°$ to the horizontal and after another, $2 \mathrm{s}$ it is traveling horizontally. The magnitude of the initial velocity of the stone is (Acceleration due to gravity, $g=10 \mathrm{m} {\mathrm{s}}^{-2}$)

A ball is projected vertically up from the ground. The boy $A$ standing at the window of the first floor of a nearby building observes that the time interval between the ball crossing him while going up and the ball crossing him while going down is $2 \mathrm{s}$. Another boy $B$ standing on the second floor notices that time interval between the ball passing him twice, during up motion and down motion is $1 \mathrm{s}$. Calculate the difference between the vertical positions of boy $B$ and boy $A$ (Assume, acceleration due to gravity, $g=10 \mathrm{m} {\mathrm{s}}^{-2}$)

Two particles are simultaneously projected in the horizontal direction from a point $P$ at a certain height. The initial velocities of the particles are oppositely directed to each other and have magnitude $v$ each. The separation between the particles at a time when their position vectors (drawn from the point $P$) are mutually perpendicular, is