Embibe Experts Solutions for Chapter: Surface Areas and Volumes, Exercise 1: CBSE-2022 (Delhi - II)

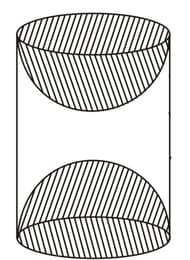
A wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in figure. If the height of the cylinder is $10 \mathrm{c}\mathrm{m}$, and its base is of radius $3.5 \mathrm{c}\mathrm{m}$. Find the total surface area of the article.

A heap of rice in the form of a cone of base diameter $24 \mathrm{m}$ and height $3.5 \mathrm{m}$. Find the volume of rice. How much canvas cloth is required to just cover the heap?

The diameters of the lower and upper ends of a bucket in the form of frustum of a cone are $10 \mathrm{cm}$ and $30 \mathrm{cm}$ respectively. If its height is $24 \mathrm{cm}$, find

(i) the area of the metal sheet used to make the bucket.

(ii) Why we should avoid the bucket made by ordinary plastic? [Use $\mathrm{\pi }=3.14$]

Water in a canal, $6 \mathrm{m}$ wide and $1.5 \mathrm{m}$ deep, is flowing with a speed of $10 \mathrm{km}/\mathrm{hour}$. How much area will it irrigate in $30$ minutes; if $8 \mathrm{cm}$ standing water is needed? (write answer in ${\mathrm{m}}^2$)

A bucket open at the top is in the form of a frustum of a cone with a capacity of $12308.8 {\mathrm{cm}}^3$. The radii of the top and bottom of circular ends of the bucket are $20 \mathrm{cm}$ and $12 \mathrm{cm}$ respectively. Find the height of the bucket and also the area of the metal sheet used in making it.(Use $\mathrm{\pi }=3.14$)

Two cones have their heights in the ratio of $1:3$ and radii in the ratio $3:1$. What is the ratio of their volumes?

A cone of base radius $4 \mathrm{cm}$ is divided into two parts by drawing a plane through the mid-point of its height and parallel to its base. Compare the volume of the two parts. 

A bucket in the form of a frustum of a cone of height $30 \mathrm{cm}$ with radii of its lower and upper ends as $10 \mathrm{cm}$ and $20 \mathrm{cm}$, respectively. Find the capacity of the bucket. Also find the cost of milk which can completely fill the bucket at the rate of $₹40$ per litre. $\left(\mathrm{Use} \mathrm{\pi }=\frac{22}{7}\right)$