Embibe Experts Solutions for Chapter: Area under Curves, Exercise 4: Exercise-4
Embibe Experts Mathematics Solutions for Exercise - Embibe Experts Solutions for Chapter: Area under Curves, Exercise 4: Exercise-4
Attempt the free practice questions on Chapter 31: Area under Curves, Exercise 4: Exercise-4 with hints and solutions to strengthen your understanding. Alpha Question Bank for Engineering: Mathematics solutions are prepared by Experienced Embibe Experts.
Questions from Embibe Experts Solutions for Chapter: Area under Curves, Exercise 4: Exercise-4 with Hints & Solutions
Let be a triangle with vertices and If be the region consisting of all these points and point inside which satisfy max. where denotes the distance of the point from the line Sketch the region and find its area.
Find the area of the region which contains all the points satisfying the condition and
Find the area of the region which is inside the parabola out side the parabola and left of the straight line
Consider the curve cuts the -axis at
The area bounded by the curve and the positive -axis between the origin and the line
The area bounded by the curve and the negative -axis between the line and the origin. Prove that
Area bounded by the line curve and the lines is Find for
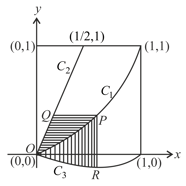
Let and be the graphs of the functions and respectively. Let be the graph of a function For a point on let the lines through parallel to the axes, meet and at and respectively (see figure).
If for every position of (on ), the areas of the shaded regions and are equal, determine the function
Given the parabola . If the circle centred at -axis with radius touches parabola at two distinct points, then find the coordinate of the centre of the circle and the area of the figure surrounded by and .
If is a quadratic function and its maximum value occurs at a point is a point of intersection of with -axis and point is such that chord subtends a right angle at Find the area enclosed by and chord
