Embibe Experts Solutions for Exercise 6: EXERCISE 6.6

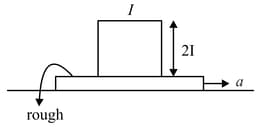
A rectangular plate is placed on a rough plank. Dimensions of the plank is as shown in the figure. Find the minimum acceleration with which the plank should be moved so that the rectangular plate topples (consider the friction is sufficient so the plate does not slide).

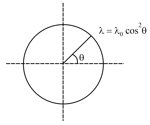
Linear mass density of a rod varies as $\lambda =kx$. Among the axes shown, the moment of inertia of the rod is maximum for

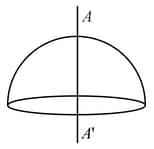
Find the moment of inertia of a solid hemisphere of mass $M$ and radius $R$ about $A{A}^{\text{'}}$

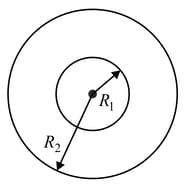
A disc of radius $R_1$ is cut out from a disc of radius $R_2$ as shown in figure. If the remaining portion of the disc has mass M then find the moment of inertia of the disc left about an axis passing through its centre and perpendicular to its plane.

Moment of inertia of a hollow sphere of mass $M$ and inner radius $R$ and outer radius $2R$ having uniform mass distribution about diameter axis is

Moment of inertia of a uniform rod of length $L$ and mass $M,$about  an axis passing through $L/4$ from one end and perpendicular to its length is 

Moment of inertia of a ring of radius $R$ whose mass per unit length varies with parametric angle $\theta$ according to relation $\lambda ={\lambda }_0{\cos }^2\theta$, about its axis will be

A square plate is thrown horizontally on a rough horizontal surface. Find the minimum value of coefficient of friction so that the plate topples.