Maharashtra Board Solutions for Chapter: Circle, Exercise 6: Problem set 3
Maharashtra Board Mathematics Solutions for Exercise - Maharashtra Board Solutions for Chapter: Circle, Exercise 6: Problem set 3
Attempt the practice questions on Chapter 3: Circle, Exercise 6: Problem set 3 with hints and solutions to strengthen your understanding. Geometry Standard X solutions are prepared by Experienced Embibe Experts.
Questions from Maharashtra Board Solutions for Chapter: Circle, Exercise 6: Problem set 3 with Hints & Solutions
In the adjoining figure circles with centres and touch each other at point . A secant passing through intersects the circles at points and respectively. Prove that, radius radius . Fill in the blanks and complete the proof.
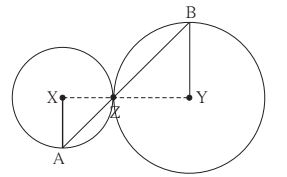
Construction: Draw segments and ........
Proof: By theorem of touching circles, points are ......
......... opposite angles
let ..........
Now .........(..........)
.......... ............(isosceles triangle theorem)
Similarly, ........... ...........(..............)
......... ...........(.........)
From
.........
radius radius ..........(........)
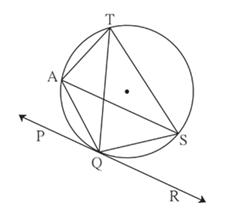
In figure line touches the circle at point . Answer the question with the help of the figure.
, find the measure of and an arc ?
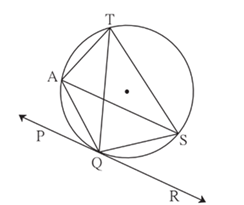
In figure line touches the circle at point . Answer the question with the help of the figure.
, find the measure of and an arc ?
In the figure, if , , find .
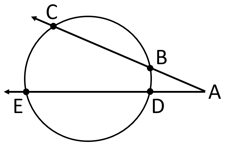
In figure, chord chord . Prove that, chord chord . Fill in the blanks and write the proof.
Proof: Draw .
_____
_____ inscribed angle theorem
_____ inscribed angle theorem
_____ from
chord chord _____.
In figure, is the point of contact of the tangent with the circle.
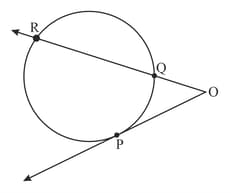
If find .
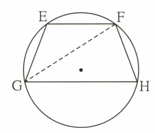
In figure, is a diameter of a circle with centre . The bisector of intersects the circle at point Prove that, . Complete the following proof by filling in the blanks.
Proof: Draw seg .
_____ angle inscribed in a semicircle.
_____ is the bisector of
_____ inscribed angle theorem
_____ definition of measure of an arc
_____
line is _____ of _____ from and
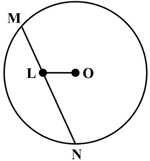
In the figure, is a chord of a circle with centre units. is a point on chord such that units and units. Find the radius of the circle in units.