Arun Sharma Solutions for Exercise 3: Extra Practice Exercise on Geometry and Mensuration
Arun Sharma Quantitative Aptitude Solutions for Exercise - Arun Sharma Solutions for Exercise 3: Extra Practice Exercise on Geometry and Mensuration
Attempt the practice questions from Exercise 3: Extra Practice Exercise on Geometry and Mensuration with hints and solutions to strengthen your understanding. How to prepare for Quantitative Aptitude solutions are prepared by Experienced Embibe Experts.
Questions from Arun Sharma Solutions for Exercise 3: Extra Practice Exercise on Geometry and Mensuration with Hints & Solutions
If the sides of a triangle measures 13, 14, 15 cm respectively, what is the height of the triangle for the base is 14.
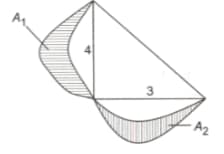
A right angled triangle is drawn on a plane such that sides adjacent to right angle are and . Now three semi-circles are drawn taking all three sides of the triangle as diameters respectively (as shown in the figure). What is the area of the shaded regions
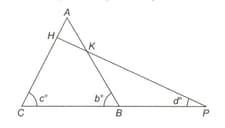
In the figure given below, and . Calculate .
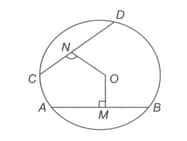
In the figure, is the centre of the circle. , and is parallel to . Find the area of the shaded region.
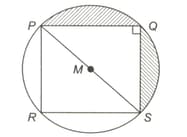
In the given figure, and are straight lines. If , , the value of is
Six solid hemispherical balls have to be arranged one upon the other vertically. Find the minimum total surface area of the cylinder in which the hemispherical balls can be arranged, if the radii of each hemispherical ball is
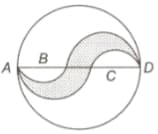
On a semicircle with diameter Chord is parallel to the diameter. Further each of the chords and has Length while has length Find the length of
In the given figure, and are points on the diameter of the circle such that Then find the ratio of area of the shaded portion to that of the whole circle.