B Nirmala Shastry Solutions for Exercise 1: EXERCISE 14A
B Nirmala Shastry Mathematics Solutions for Exercise - B Nirmala Shastry Solutions for Exercise 1: EXERCISE 14A
Attempt the practice questions from Exercise 1: EXERCISE 14A with hints and solutions to strengthen your understanding. ICSE MATHEMATICS CLASS 9 solutions are prepared by Experienced Embibe Experts.
Questions from B Nirmala Shastry Solutions for Exercise 1: EXERCISE 14A with Hints & Solutions
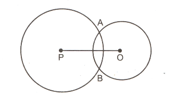
The length of the common chord of two intersecting circles is . If the diameters of the circles are , calculate the distance between the centres.
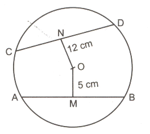
In the given circle with centre , and . Find the radius of the circle.
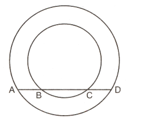
In the given figure, is the chord of the larger of the two concentric circles and is the chord of the smaller circle. Prove that .
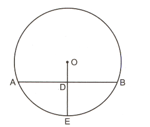
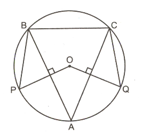
Triangle is inscribed in a circle with centre and . Prove that .
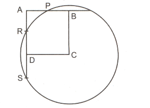
is a square, is the centre of the circle. Prove that .
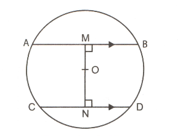
In the figure given above, and are two parallel chords and is the centre. If the radius of the circle is , find the distance between the two chords of length and respectively.
In the given figure, is the centre of the circle. and are two chords of the circle. is perpendicular to and is perpendicular to . . Find the radius of the circle.
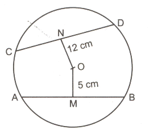
In the given figure, is the centre of the circle. and are two chords of the circle. is perpendicular to and is perpendicular to . . Find the length of chord .